
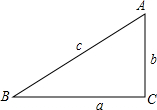
 如图,在Rt△ABC中,∠C=90°,∠A、∠B、∠C所对的边分别用a、b、c表示,我们定义:锐角∠A的对边a与斜边c的比值$\frac{a}{c}$叫做∠A的正弦值,记为:sinA=$\frac{a}{c}$.如果某个直角三角形中,a=4,c=5,则∠A的正弦值为$\frac{4}{5}$,记为:sinA=$\frac{4}{5}$.如果某直角三角形中,∠A=60°,则sinA是( )
如图,在Rt△ABC中,∠C=90°,∠A、∠B、∠C所对的边分别用a、b、c表示,我们定义:锐角∠A的对边a与斜边c的比值$\frac{a}{c}$叫做∠A的正弦值,记为:sinA=$\frac{a}{c}$.如果某个直角三角形中,a=4,c=5,则∠A的正弦值为$\frac{4}{5}$,记为:sinA=$\frac{4}{5}$.如果某直角三角形中,∠A=60°,则sinA是( )| A. | 1 | B. | 0 | C. | $\frac{1}{2}$ | D. | $\frac{\sqrt{3}}{2}$ |
分析 在Rt△ABC中,∠C=90°,∠A=60°,∠A、∠B、∠C所对的边分别用a、b、c表示,则c=2b,利用勾股定理计算出a=$\sqrt{3}$b,然后根据正弦的定义求解.
解答 解:在Rt△ABC中,∠C=90°,∠A=60°,∠A、∠B、∠C所对的边分别用a、b、c表示,则c=2b,a=$\sqrt{{c}^{2}-{a}^{2}}$=$\sqrt{3}$b,
所以sinA=$\frac{a}{c}$=$\frac{\sqrt{3}b}{2b}$=$\frac{\sqrt{3}}{2}$.
故选D.
点评 本题考查了锐角三角函数的定义:在Rt△ABC中,∠C=90°,锐角∠A的对边a与斜边c的比值$\frac{a}{c}$叫做∠A的正弦值,记为:sinA=$\frac{a}{c}$.


科目:初中数学 来源:2017届四川省遂宁市九年级上学期期末考试数学试卷(解析版) 题型:解答题
如图,二次函数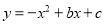 的图象经过坐标原点,与
的图象经过坐标原点,与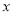 轴的另一个交点为A(-2,0).
轴的另一个交点为A(-2,0).

(1)求二次函数的解析式
(2)在抛物线上是否存在一点P,使△AOP的面积为3,若存在请求出点P的坐标,若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源:2016-2017学年广东省东莞市堂星晨学校七年级3月月考数学试卷(解析版) 题型:解答题
如图,B村位于一条河的一岸,现在要将河里的水通过修建水渠引到村里进行使用,问:这条水渠该如何修,才能使到A村的距离最短,请画出图形,并说明理由?(画图可借助三角板,量角器等工具)
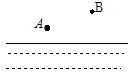
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 把二次函数y=$\frac{1}{2}$x2-3x+4配方成y=a(x-k)2+h的形式,并求出它的图象的顶点坐标、对称轴方程,并画出图象.
把二次函数y=$\frac{1}{2}$x2-3x+4配方成y=a(x-k)2+h的形式,并求出它的图象的顶点坐标、对称轴方程,并画出图象.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com