
【题目】已知:点A、C分别是∠B的两条边上的点,点D、E分别是直线BA、BC上的点,直线AE、CD相交于点P.
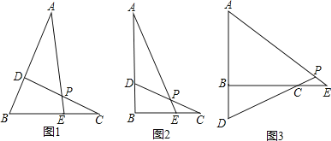
(1)点D、E分别在线段BA、BC上;
①若∠B=60°(如图1),且AD=BE,BD=CE,则∠APD的度数为 ;
②若∠B=90°(如图2),且AD=BC,BD=CE,求∠APD的度数;
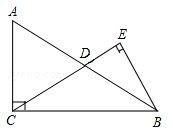
(2)如图3,点D、E分别在线段AB、BC的延长线上,若∠B=90°,AD=BC,∠APD=45°,求证:BD=CE.
【答案】(1)①60°;②45°;(2)见解析
【解析】
(1)连结AC,由条件可以得出△ABC为等边三角形,再由证△CBD≌△ACE就可以得出∠BCD=∠CAE,就可以得出结论;
(2)作AF⊥AB于A,使AF=BD,连结DF,CF,就可以得出△FAD≌△DBC,再证△DCF为等腰直角三角形,由∠FAD=∠B=90°,就可以得出AF∥BC,就可以得出四边形AECF是平行四边形,就有AE∥CF,就可以得出∠EAC=∠FCA,就可以得出结论;
(3)作AF⊥AB于A,使AF=BD,连结DF,CF,就可以得出△FAD≌△DBC,再证△DCF为等腰直角三角形,就有∠DCF=∠APD=45°,推出CF∥AE,由∠FAD=∠B=90°,就可以得出AF∥BC,就可以得出四边形AFCE是平行四边形,就有AF=CE.
(1)①如图1,连结AC,
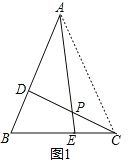
∵AD=BE,BD=CE,
∴AD+BD=BE+CE,
∴AB=BC.
∵∠B=60°,
∴△ABC为等边三角形.
∴∠B=∠ACB=60°,BC=AC.
在△CBD和△ACE中
 ,
,
∴△CBD≌△ACE(SAS),
∴∠BCD=∠CAE.
∵∠APD=∠CAE+∠ACD,
∴∠APD=∠BCD+∠ACD=60°.
故答案为60°;
②如图2,作AF⊥AB于A,使AF=BD,连结DF,CF,

∴∠FAD=90°.
∵∠B=90°,
∴∠FAD=∠B.
在△FAD和△DBC中,
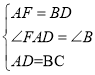 ,
,
∴△FAD≌△DBC(SAS),
∴DF=DC,∠ADF=∠BCD.
∵∠BDC+∠BCD=90°,
∴∠ADF+∠BDC=90°,
∴∠FDC=90°,
∴∠FCD=45°.
∵∠FAD=90°,∠B=90,
∴∠FAD+∠B=180°,
∴AF∥BC.
∵DB=CE,
∴AF=CE,
∴四边形AECF是平行四边形,
∴AE∥CF,
∴∠EAC=∠FCA.
∵∠APD=∠ACP+∠EAC,
∴∠APD=∠ACP+∠ACE=45°;
(2)如图3,作AF⊥AB于A,使AF=BD,连结DF,CF,
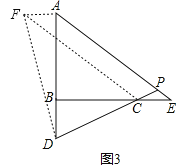
∴∠FAD=90°.
∵∠ABC=90°,
∴∠FAD=∠DBC=90°.
在△FAD和△DBC中,
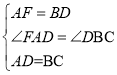 ,
,
∴△FAD≌△DBC(SAS),
∴DF=DC,∠ADF=∠BCD.
∵∠BDC+∠BCD=90°,
∴∠ADF+∠BDC=90°,
∴∠FDC=90°,
∴∠FCD=45°.
∵∠APD=45°,
∴∠FCD=∠APD,
∴CF∥AE.
∵∠FAD=90°,∠ABC=90,
∴∠FAD=∠ABC,
∴AF∥BC.
∴四边形AECF是平行四边形,
∴AF=CE,
∴CE=BD.


科目:初中数学 来源: 题型:
【题目】如图在Rt△ABC中,∠ACB=90°,D是边AB的中点,BE⊥CD,垂足为点E.已知AC=15,cosA=![]() .
.
(1)求线段CD的长;
(2)求sin∠DBE的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,抛物线的表达式为
中,抛物线的表达式为![]() ,线段AB的两个端点分别为A(1,2),B(3,2)
,线段AB的两个端点分别为A(1,2),B(3,2)
(1)若抛物线经过原点,求出![]() 的值;
的值;
(2)求抛物线顶点C的坐标(用含有m的代数式表示);
(3)若抛物线与线段AB恰有一个公共点,结合函数图象,求出m的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,以原点为对称中心,把点A(3,4)逆时针旋转90°,得到点B,则点B的坐标为()
A. (4,-3) B. (-4,3) C. (-3,4) D. (-3,-4)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,平行四边形ABCD的周长为28,对角线AC、BD相交于点O,点E是CD的中点,BD=12,则△DOE的周长为( )

A.28B.12C.13D.17
查看答案和解析>>
科目:初中数学 来源: 题型:
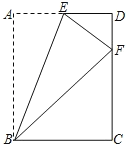
【题目】如图,矩形ABCD的边BC和AB的长分别为4和5,把它的左上角如图所示折叠.点A恰好落在CD边上的点F处,折痕为BE,则DE的长为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
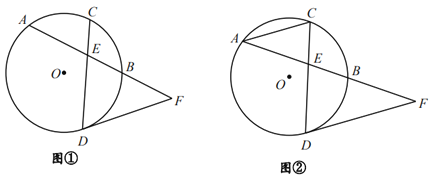
【题目】如图,已知,⊙O的半径![]() ,弦AB,CD交于点E,C为
,弦AB,CD交于点E,C为![]() 的中点,过D点的直线交AB延长线与点F,且DF=EF.
的中点,过D点的直线交AB延长线与点F,且DF=EF.
(1)如图①,试判断DF与⊙O的位置关系,并说明理由;
(2)如图②,连接AC,若AC∥DF,BE=![]() AE,求CE的长.
AE,求CE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,利用两面靠墙(墙足够长),用总长度37米的篱笆(图中实线部分)围成一个矩形鸡舍ABCD,且中间共留三个1米的小门,设篱笆BC长为x米.
(1)AB=______.(用含x的代数式表示)
(2)若矩形鸡舍ABCD 面积为150平方米,求篱笆BC的长.
(3)矩形鸡舍ABCD面积是否有可能达到210平方米?若有可能,求出相应x的值;若不可能,则说明理由.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com