练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

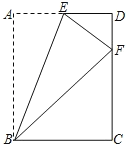
    【题目】如图，矩形ABCD的边BC和AB的长分别为4和5，把它的左上角如图所示折叠．点A恰好落在CD边上的点F处，折痕为BE，则DE的长为(　　)

    A.B.C.D.

    【答案】A

    【解析】

    根据折叠的性质可得BF=AB，EF=AE，在Rt△BFC中根据勾股定理求出CF，从而求出DF，在Rt△DEF中根据勾股定理即可求得EF=AE，从而求得DE．

    解：∵四边形ABCD是矩形，

    ∴AB=CD=5，AD=BC=4．

    ∵把它的左上角如图所示折叠．点A恰好落在CD边上的点F处，折痕为BE，

    ∴AE=EF，BF=AB=5，

    ∴CF3，

    ∴DF=5﹣3=2．

    ∵DE2+DF2=EF2，

    ∴(4﹣EF)2+22=EF2，

    ∴EF，

    ∴DE=AD﹣AE=AD﹣EF．

    故选：A．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】如图是学习分式方程应用时，老师板书的问题和两名同学所列的方程．

    根据以上信息，解答下列问题．

    （1）冰冰同学所列方程中的x表示什么，庆庆同学所列方程中的y表示什么；

    （2）两个方程中任选一个，并写出它的等量关系；

    （3）解（2）中你所选择的方程，并回答老师提出的问题．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】下表显示的是某种大豆在相同条件下的发芽试验结果：

    每批粒数n

    100

    300

    400

    600

    1000

    2000

    3000

    发芽的粒数m

    96

    282

    382

    570

    948

    1904

    2850

    发芽的频率

    0.960

    0.940

    0.955

    0.950

    0.948

    0.952

    0.950

    下面有三个推断：

    ①当n为400时，发芽的大豆粒数为382，发芽的频率为0.955，所以大豆发芽的概率是0.955；

    ②随着试验时大豆的粒数的增加，大豆发芽的频率总在0.95附近摆动，显示出一定的稳定性，可以估计大豆发芽的概率是0.95；

    ③若大豆粒数n为4000，估计大豆发芽的粒数大约为3800粒．

    其中推断合理的是（　　）

    A. ①②③ B. ①② C. ①③ D. ②③

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】已知：点A、C分别是∠B的两条边上的点，点D、E分别是直线BA、BC上的点，直线AE、CD相交于点P．

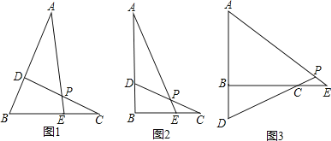
    （1）点D、E分别在线段BA、BC上；

    ①若∠B＝60°（如图1），且AD＝BE，BD＝CE，则∠APD的度数为　 　；

    ②若∠B＝90°（如图2），且AD＝BC，BD＝CE，求∠APD的度数；

    （2）如图3，点D、E分别在线段AB、BC的延长线上，若∠B＝90°，AD＝BC，∠APD＝45°，求证：BD＝CE．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】已知一次函数y=mx+n与反比例函数y=其中m、n为常数，且mn＜0，则它们在同一坐标系中的图象可能是（　　）

    A. B. C. D.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

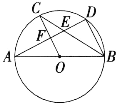
    【题目】如图所示，AB是⊙O的直径，C、D是⊙O上的点，且OC∥BD, AD分别与BC，OC相交于点E，F，则下列结论：①AD⊥BD; ②∠AOC=∠AEC; ③CB平分∠ABD;④AF=DF; ⑤BD=2OF; ⑥△CEF ≌△BED,其中一定成立的是（ ）

    A. ① ③ ⑤ ⑥ B. ① ③ ④ ⑤

    C. ② ④ ⑤ ⑥ D. ② ③ ④ ⑥

    查看答案和解析>>

    科目：初中数学 来源： 题型：

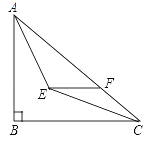
    【题目】如图，在Rt△ABC中，∠ABC=90°，AB=6，BC=8，∠BAC与∠ACB的平分线相较于点E，过点E作EF∥BC交AC于点F，则EF的长为________．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在△AOB中，∠AOB＝90°，点A的坐标为（4，2），BO＝4，反比例函数y＝的图象经过点B，则k的值为_____．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，PA、PB是⊙O的两条切线，A、B是切点，AC是⊙O的直径，∠BAC＝35°，求∠P的度数．

    查看答案和解析>>

    同步练习册答案