
【题目】如图是学习分式方程应用时,老师板书的问题和两名同学所列的方程.

根据以上信息,解答下列问题.
(1)冰冰同学所列方程中的x表示什么,庆庆同学所列方程中的y表示什么;
(2)两个方程中任选一个,并写出它的等量关系;
(3)解(2)中你所选择的方程,并回答老师提出的问题.
【答案】(1)甲队每天修路的长度;甲队修路400米所需时间;(2)冰冰用的等量关系是:甲队修路400米所用时间=乙队修路600米所用时间;(3)甲队每天修路的长度为40米.
【解析】
(1)根据两人的方程思路,可得出:x表示甲队每天修路的长度;y表示甲队修路400米所需时间;
(2)根据题意,可找出:(冰冰)甲队修路400米所用时间=乙队修路600米所用时间;(庆庆)乙队每天修路的长度﹣甲队每天修路的长度=20米;
(3)选择两个方程中的一个,解之即可得出结论.
解:(1)∵冰冰是根据时间相等列出的分式方程,
∴x表示甲队每天修路的长度;
∵庆庆是根据乙队每天比甲队多修20米列出的分式方程,
∴y表示甲队修路400米所需时间.
故答案为:甲队每天修路的长度;甲队修路400米所需时间.
(2)冰冰用的等量关系是:甲队修路400米所用时间=乙队修路600米所用时间;
庆庆用的等量关系是:乙队每天修路的长度﹣甲队每天修路的长度=20米(选择一个即可).
(3)选冰冰的方程:![]() =
=![]() ,
,
去分母,得:400x+8000=600x,
移项,x的系数化为1,得:x=40,
检验:当x=40时,x、x+20均不为零,
∴x=40.
答:甲队每天修路的长度为40米.
选庆庆的方程:![]() -
-![]() =20,
=20,
去分母,得:600﹣400=20y,
将y的系数化为1,得:y=10,
经验:当y=10时,分母y不为0,
∴y=10,
∴![]() =40.
=40.
答:甲队每天修路的长度为40米.
故答案为:(1)甲队每天修路的长度;甲队修路400米所需时间;(2)冰冰用的等量关系是:甲队修路400米所用时间=乙队修路600米所用时间;(3)甲队每天修路的长度为40米.


 提分百分百检测卷系列答案
提分百分百检测卷系列答案 宝贝计划期末冲刺夺100分系列答案
宝贝计划期末冲刺夺100分系列答案 能考试全能100分系列答案
能考试全能100分系列答案科目:初中数学 来源: 题型:
【题目】已知抛物线F:y=x2+bx+c的图象经过坐标原点O,且与x轴另一交点为(![]() ,0).
,0).

(1)求抛物线F的解析式;
(2)如图1,直线l:y![]() x+m(m>0)与抛物线F相交于点A(x1,y1)和点B(x2,y2)(点A在第二象限),求y2﹣y1的值(用含m的式子表示);
x+m(m>0)与抛物线F相交于点A(x1,y1)和点B(x2,y2)(点A在第二象限),求y2﹣y1的值(用含m的式子表示);
(3)在(2)中,若m![]() ,设点A′是点A关于原点O的对称点,如图2.
,设点A′是点A关于原点O的对称点,如图2.
①判断△AA′B的形状,并说明理由;
②平面内是否存在点P,使得以点A、B、A′、P为顶点的四边形是菱形?若存在,求出点P的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】动画片《小猪佩奇》分靡全球,受到孩子们的喜爱.现有4张《小猪佩奇》角色卡片,分别是A佩奇,B乔治,C佩奇妈妈,D佩奇爸爸(四张卡片除字母和内容外,其余完全相同).姐弟两人做游戏,他们将这四张卡片混在一起,背面朝上放好.
(1)姐姐从中随机抽取一张卡片,恰好抽到A佩奇的概率为 ;
(2)若两人分别随机抽取一张卡片(不放回),请用列表或画树状图的分方法求出恰好姐姐抽到A佩奇弟弟抽到B乔治的概率.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】二次函数y=ax2+bx+c(a≠0)的图象如图所示,下列结论:①b2﹣4ax>0;②2a+b>0;③abc<0;④4a﹣2b+c<0;⑤a+b+c>0.其中正确的个数是( )
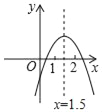
A. 2个 B. 3个 C. 4个 D. 5个
查看答案和解析>>
科目:初中数学 来源: 题型:
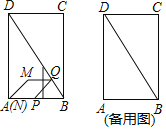
【题目】如图,在矩形ABCD中,AB=2cm,∠ADB=30°.P,Q两点分别从A,B同时出发,点P沿折线AB﹣BC运动,在AB上的速度是2cm/s,在BC上的速度是2![]() cm/s;点Q在BD上以2cm/s的速度向终点D运动,过点P作PN⊥AD,垂足为点N.连接PQ,以PQ,PN为邻边作PQMN.设运动的时间为x(s),PQMN与矩形ABCD重叠部分的图形面积为y(cm2)
cm/s;点Q在BD上以2cm/s的速度向终点D运动,过点P作PN⊥AD,垂足为点N.连接PQ,以PQ,PN为邻边作PQMN.设运动的时间为x(s),PQMN与矩形ABCD重叠部分的图形面积为y(cm2)
(1)当PQ⊥AB时,x等于多少;
(2)求y关于x的函数解析式,并写出x的取值范围;
(3)直线AM将矩形ABCD的面积分成1:3两部分时,直接写出x的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,在四张背面完全相同的纸牌的正面分别画有四个不同的几何图形,将这四张纸牌背面朝上洗匀后摸出一张,不放回,再摸出一张
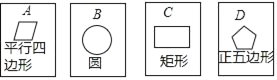
(1)用树状图(或列表法)表示两次摸牌所有可能出现的结果(纸牌可用A、B、C、D表示);
(2)求摸出的两张纸牌牌面上所画几何图形既是轴对称图形又是中心对称图形的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图在Rt△ABC中,∠ACB=90°,D是边AB的中点,BE⊥CD,垂足为点E.已知AC=15,cosA=![]() .
.
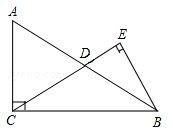
(1)求线段CD的长;
(2)求sin∠DBE的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
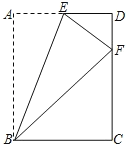
【题目】如图,矩形ABCD的边BC和AB的长分别为4和5,把它的左上角如图所示折叠.点A恰好落在CD边上的点F处,折痕为BE,则DE的长为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com