
【题目】小林有3张扑克牌,小丽有2张扑克牌,扑克牌上的数字如图所示。两人用这些扑克牌做游戏,他们分别从自己的扑克牌中随机抽取一张。
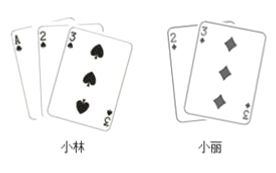
(1)求两人抽取的扑克牌上的数字之积为奇数的概率;(用“列表”或“画树状图”的方法说明);
(2)若两人抽取的扑克牌上的数字之积为奇数,则小林胜,否则小丽胜,这个游戏公平吗?若不公平,请修改游戏规则,使得游戏公平;若公平,请说明理由。
【答案】(1)![]() ;(2)不公平,修改规则:若两人抽取的扑克牌上的数字之和为奇数,则小林胜,否则小丽胜,此时P(小林获胜)= P(小丽获胜)
;(2)不公平,修改规则:若两人抽取的扑克牌上的数字之和为奇数,则小林胜,否则小丽胜,此时P(小林获胜)= P(小丽获胜)![]() .
.
【解析】
(1)首先根据题意画出树状图,然后由树状图求得所有等可能的结果,再利用概率公式求解即可求得答案;
(2)根据概率公式先求出小林和小丽获胜的概率,再进行比较得出游戏的公平性,要游戏公平,关键要看是否游戏双方各有50%赢的机会,然后进行修改即可.
(1)根据题意画图如下:
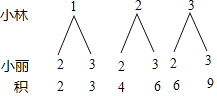
∵共有6种等可能的结果,两人抽取的扑克牌上的数字之积为奇数的有2种情况,
∴P(数字之积为奇数)=![]() ;
;
(2)由(1)得P(小林获胜)![]() ,
,
∴P(小丽获胜)![]() ,
,
∵![]() ,
,
∴不公平,
修改规则:若两人抽取的扑克牌上的数字之和为奇数,则小林胜,否则小丽胜,此时P(小林获胜)= P(小丽获胜)![]() .
.


 七彩题卡口算应用一点通系列答案
七彩题卡口算应用一点通系列答案科目:初中数学 来源: 题型:
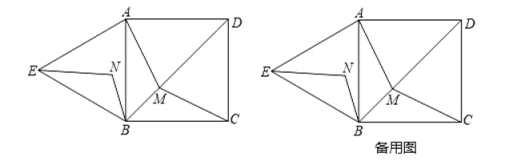
【题目】 如图,梯形ABCD中,AB//CD,且AB=2CD,E,F分别是AB,BC的中点.
EF与BD相交于点M.

(1)求证:△EDM∽△FBM;
(2)若DB=9,求BM.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某汽车租贸公司共有汽车50辆,市场调查表明,当租金为每辆每日200元时可全部租出,当租金每提高10元,租出去的车就减少2辆.
(1)当租金提高多少元时,公司的每日收益可达到10120元?
(2)公司领导希望日收益达到10160元,你认为能否实现?若能,求出此时的租金,若不能,请说明理由,
(3)汽车日常维护要定费用,已知外租车辆每日维护费为100元未租出的车辆维护费为50元,当租金为多少元时,公司的利润恰好为5500元?(利润=收益﹣维护费)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】关于下列说法:(1)反比例函数![]() ,在每个象限内
,在每个象限内![]() 随
随![]() 的增大而减小;(2)函数
的增大而减小;(2)函数![]() ,
,![]() 随
随![]() 的增大减小;(3)函数
的增大减小;(3)函数![]() ,当
,当![]() 时,
时,![]() 随
随![]() 的增大而减小,其中正确的有( )
的增大而减小,其中正确的有( )
A.0个B.1个C.2个D.3个
查看答案和解析>>
科目:初中数学 来源: 题型:
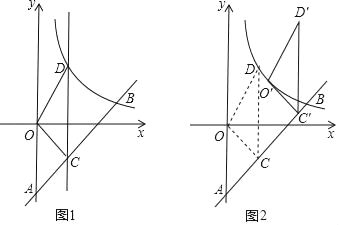
【题目】如图1,一次函数y=kx﹣6(k≠0)的图象与y轴交于点A,与反比例函数y=![]() (x>0)的图象交于点B(4,b).
(x>0)的图象交于点B(4,b).
(1)b= ;k= ;
(2)点C是线段AB上一点,过点C且平行于y轴的直线l交该反比例函数的图象于点D,连接OC,OD,BD,若四边形OCBD的面积S四边形OCBD=![]() ,求点C的坐标;
,求点C的坐标;
(3)将第(2)小题中的△OCD沿射线AB方向平移一定的距离后,得到△O'C'D',若点O的对应点O'恰好落在该反比例函数图象上(如图2),求此时点D的对应点D'的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
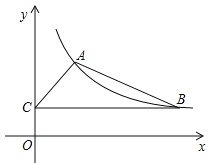
【题目】如图,某反比例函数图象的一支经过点A(2,3)和点B(点B在点A的右侧),作BC⊥y轴,垂足为点C,连结AB,AC.
(1)求该反比例函数的解析式;
(2)若△ABC的面积为6,求直线AB的表达式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形![]() 是正方形,
是正方形,![]() 是等边三角形,
是等边三角形,![]() 为对角线
为对角线![]() (不含
(不含![]() 点)上任意一点,将
点)上任意一点,将![]() 绕点
绕点![]() 逆时针旋转
逆时针旋转![]() 得到
得到![]() ,连接
,连接![]() 、
、![]() 、
、![]() .设点
.设点![]() 的坐标为
的坐标为![]() .
.
(1)若建立平面直角坐标系,满足原点在线段![]() 上,点
上,点![]() ,
,![]() .且
.且![]() (
(![]() ),则点
),则点![]() 的坐标为 ,点
的坐标为 ,点![]() 的坐标为 ;请直接写出点
的坐标为 ;请直接写出点![]() 纵坐标
纵坐标![]() 的取值范围是 ;
的取值范围是 ;
(2)若正方形的边长为2,求![]() 的长,以及
的长,以及![]() 的最小值. (提示:连结
的最小值. (提示:连结![]() :
:![]() ,
,![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某班学生做“用频率估计概率”的实验时,给出的某一结果出现的频率折线图,则符合这一结果的实验可能是( )
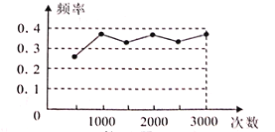
A.抛一枚硬币,出现正面朝上
B.从标有1,2,3,4,5,6的六张卡片中任抽一张,出现偶数
C.一副去掉大小王的扑克牌洗匀后,从中任抽一张牌的花色是红桃
D.从一个装有6个红球和3个黑球的袋子中任取一球,取到的是黑球
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com