
| 进价(元/只) | 售价(元/只) | |
| 甲种节能灯 | 30 | 40 |
| 乙种节能灯 | 35 | 50 |
分析 (1)利用节能灯数量和所用的价钱建立方程组即可;
(2)每种灯的数量乘以每只灯的利润,最后求出之和即可.
解答 解:(1)设商场购进甲种节能灯x只,购进乙种节能灯y只,
根据题意,得$\left\{\begin{array}{l}30x+35y=3300\\ x+y=100\end{array}\right.$,
解这个方程组,得 $\left\{\begin{array}{l}x=40\\ y=60\end{array}\right.$,
答:甲、乙两种节能灯分别购进40、60只.
(2)商场获利=40×(40-30)+60×(50-35)=1300(元),
答:商场获利1300元.
点评 此题是二元一次方程组的应用,主要考查了列方程组解应用题的步骤和方法,利润问题,解本题的关键是求出两种节能灯的数量.


科目:初中数学 来源: 题型:解答题
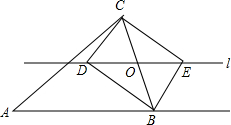 如图,∠CBF是△ABC的一个外角,点O是BC上的任意一点(不与B、C重合),过点O作直线l∥AB,且直线l与∠ABC的平分线相交于D,与∠CBF的平分线相交于E,
如图,∠CBF是△ABC的一个外角,点O是BC上的任意一点(不与B、C重合),过点O作直线l∥AB,且直线l与∠ABC的平分线相交于D,与∠CBF的平分线相交于E,查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,矩形ABCD中,∠FCD=75°,以CF为一边的等边△EFC的另一顶点E在AD上,点K是FC的中点
如图,矩形ABCD中,∠FCD=75°,以CF为一边的等边△EFC的另一顶点E在AD上,点K是FC的中点查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,正方形ABCD中,AD=8,E是对角线AC的中点,动点P从点A出发,沿AB方向以每秒1个单位的速度向终点B运动,同时动点Q从点B出发,以每秒2个单位的速度先沿BC方向运动到点C,再沿CD方向向终点D运动,连接EP,EQ,以EP、EQ为邻边作?PEQF,设点P运动的时间为t秒(t>0)
如图,正方形ABCD中,AD=8,E是对角线AC的中点,动点P从点A出发,沿AB方向以每秒1个单位的速度向终点B运动,同时动点Q从点B出发,以每秒2个单位的速度先沿BC方向运动到点C,再沿CD方向向终点D运动,连接EP,EQ,以EP、EQ为邻边作?PEQF,设点P运动的时间为t秒(t>0)查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 3-a>3-b | B. | a-3>b-3 | C. | -$\frac{a}{3}$<-$\frac{b}{3}$ | D. | a2<b2 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com