
【题目】已知等边△ABC,点D为BC上一点,连接AD.
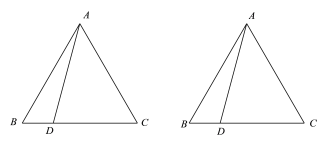
图1 图2
(1)若点E是AC上一点,且CE=BD,连接BE,BE与AD的交点为点P,在图(1)中根据题意补全图形,直接写出∠APE的大小;
(2)将AD绕点A逆时针旋转120°,得到AF,连接BF交AC于点Q,在图(2)中根据题意补全图形,用等式表示线段AQ和CD的数量关系,并证明.
【答案】(1)补全图形见解析. ∠APE=60°;(2)补全图形见解析.![]() ,证明见解析.
,证明见解析.
【解析】
(1)根据题意,按照要求补全图形即可;
(2)先补全图形,然后首先证明△ABD≌△BEC得出∠BAD=∠CBE,之后通过一系列证明得出△AQF≌△EQB,最后进一步从而得出![]() 即可.
即可.
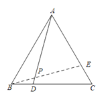
(1)补全图形如下,其中 ∠APE=60°,
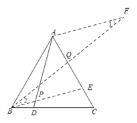
(2)补全图形.![]()
证明:在△ABD和△BEC中,
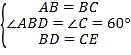
∴△ABD≌△BEC(SAS)
∴∠BAD=∠CBE.
∵∠APE是△ABP的一个外角,
∴∠APE=∠BAD+∠ABP=∠CBE+∠ABP=∠ABC=60°.
∵AF是由AD绕点A逆时针旋转120°得到,
∴AF=AD,∠DAF=120°.
∵∠APE=60°,
∴∠APE+∠DAP=180°.
∴AF∥BE
∴∠1=∠2
∵△ABD≌△BEC,
∴AD=BE.
∴AF=BE.
在△AQF和△EQB中,
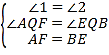
∴△AQF≌△EQB(AAS)
∴AQ=QE
∴![]()
∵AE=AC-CE,CD=BC-BD,
且AE=BC,CD=BD.
∴AE=CD..
∴![]()


科目:初中数学 来源: 题型:
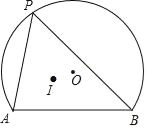
【题目】如图,AB为弓形AB的弦,AB=2![]() ,弓形所在圆⊙O的半径为2,点P为弧AB上动点,点I为△PAB的内心,当点P从点A向点B运动时,点I移动的路径长为_____.
,弓形所在圆⊙O的半径为2,点P为弧AB上动点,点I为△PAB的内心,当点P从点A向点B运动时,点I移动的路径长为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)直线l1:y=x+1与x轴交于点A,直线l2:y=﹣x+3与x轴交于点B,l1与l2交于点C,直线l3过线段AB的中点和点C,求直线l3的解析式;
(2)已知平面直角坐标系中,直线l经过点P(2,1)且与双曲线y=![]() 交于A、B不同两点,问是否存在这样的直线l,使得点P恰好为线段AB的中点,若存在,求出直线l的解析式,若不存在,请说明理由;
交于A、B不同两点,问是否存在这样的直线l,使得点P恰好为线段AB的中点,若存在,求出直线l的解析式,若不存在,请说明理由;
(3)若A(x1,y1)、B(x2,y2)是抛物线y=4x2上的不同两点(y1≠y2),线段AB的垂直平分线与y轴交于点P,与线段AB交于点M(xm,ym),则称线段AB为点P的一条“相关弦”,若点P的坐标为(0,a)时(a为常数),证明点P的“相关弦”中点M的纵坐标相同.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下面是小东设计的“过圆外一点作这个圆的两条切线”的尺规作图过程.
已知:⊙O及⊙O外一点P.
求作:直线PA和直线PB,使PA切⊙O于点A,PB切⊙O于点B.
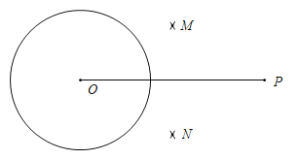
作法:如图,
①连接OP,分别以点O和点P为圆心,大于![]() OP的同样长为半径作弧,两弧分别交于点M,N;
OP的同样长为半径作弧,两弧分别交于点M,N;
②连接MN,交OP于点Q,再以点Q为圆心,OQ的长为半径作弧,交⊙O于点A和点B;
③作直线PA和直线PB.
所以直线PA和PB就是所求作的直线.
根据小东设计的尺规作图过程,
(1)使用直尺和圆规,补全图形;(保留作图痕迹)
(2)完成下面的证明.
证明:∵OP是⊙Q的直径,
∴ ∠OAP=∠OBP=________°( )(填推理的依据).
∴PA⊥OA,PB⊥OB.
∵OA,OB为⊙O的半径,
∴PA,PB是⊙O的切线.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为响应荆州市“创建全国文明城市”号召,某单位不断美化环境,拟在一块矩形空地上修建绿色植物园,其中一边靠墙,可利用的墙长不超过18m,另外三边由36m长的栅栏围成.设矩形ABCD空地中,垂直于墙的边AB=xm,面积为ym2(如图).
(1)求y与x之间的函数关系式,并写出自变量x的取值范围;
(2)若矩形空地的面积为160m2,求x的值;
(3)若该单位用8600元购买了甲、乙、丙三种绿色植物共400棵(每种植物的单价和每棵栽种的合理用地面积如下表).问丙种植物最多可以购买多少棵?此时,这批植物可以全部栽种到这块空地上吗?请说明理由.
甲 | 乙 | 丙 | |
单价(元/棵) | 14 | 16 | 28 |
合理用地(m2/棵) | 0.4 | 1 | 0.4 |

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】随着信息技术的迅猛发展,人们去商场购物的支付方式更加多样、便捷.某校数学兴趣小组设计了一份调查问卷,要求每人选且只选一种你最喜欢的支付方式.现将调查结果进行统计并绘制成如下两幅不完整的统计图,请结合图中所给的信息解答下列问题:
(1)这次活动共调查了 人;在扇形统计图中,表示“支付宝”支付的扇形圆心角的度数为 ;
(2)将条形统计图补充完整.观察此图,支付方式的“众数”是“ ”;
(3)在一次购物中,小明和小亮都想从“微信”、“支付宝”、“银行卡”三种支付方式中选一种方式进行支付,请用画树状图或列表格的方法,求出两人恰好选择同一种支付方式的概率.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某班13位同学参加每周一次的卫生大扫除,按学校的卫生要求需要完成总面积为60m2的三个项目的任务,三个项目的面积比例和每人每分钟完成各所示:项目的工作量如图:
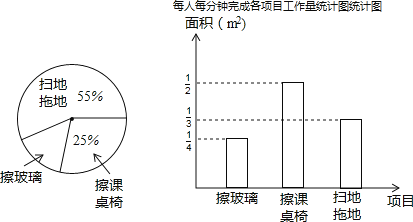
(1)从统计图中可知:擦玻璃的面积占总面积的百分比为 ,每人每分钟擦课桌椅 m2;
(2)扫地拖地的面积是 m2;
(3)他们一起完成扫地和拖地任务后,把这13人分成两组,一组去擦玻璃,一组去擦课桌椅,如果你是卫生委员,该如何分配这两组的人数,才能最快地完成任务?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com