
【题目】某班级在探究“将军饮马问题”时抽象出数学模型:
直线l同旁有两个定点A、B,在直线![]() 上存在点P,使得PA+PB的值最小.解法:如图1,作点A关于直线
上存在点P,使得PA+PB的值最小.解法:如图1,作点A关于直线![]() 的对称点
的对称点![]() ,连接
,连接![]() ,则
,则![]() 与直线l的交点即为P,且PA+PB的最小值为
与直线l的交点即为P,且PA+PB的最小值为![]() .
.


请利用上述模型解决下列问题:
(1)几何应用:如图2,△ABC中,∠C=90°,AC=BC=2,E是AB的中点,P是BC边上的一动点,则PA+PE的最小值为 ;
(2)代数应用:求代数式![]() +
+![]() (0≤x≤3)的最小值.
(0≤x≤3)的最小值.
(3)几何拓展:如图3,△ABC中,AC=2,∠A=30°,若在AB、AC上各取一点M、N使BM+MN的值最小,最小值是 ;
【答案】(1)![]() .(2)5.(3)
.(2)5.(3)![]() .
.
【解析】
(1)根据轴对称-最短路线问题解答;
(2)作点A关于BC的对称点D,连接ED交BC于P,则PA+PE的值最小,连接BD,根据勾股定理求出DE即可.
(3)设点B关于AC的对称点为B′,根据垂线段最短及两点之间,线段最短可知当B′、M、N三点共线且B′N⊥AB时BM+MN的值最小.
(1)
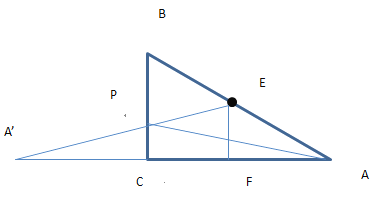
如图,PA+PE的最小值为A’E的长度
作EF⊥AC,∵E是AB的中点
∴EF=![]() ,
,![]()
∴![]()
![]() .
.
(2)构造图形如图所示,
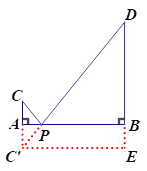
其中:AB=3,AC=1,DB=3,AP=x,CA⊥AB于A,DB⊥AB于B.
∵PC+PD=![]() +
+![]() ,
,
∴所求的最小值就是求PC+PD的最小值.
作点C关于AB的对称点C',过C' 作C' E垂直DB的延长线于E.
则C' E=AB=3,DE=3+1=4,C' D=![]() =5
=5
∴所求代数式的最小值是5.
(3)作点B关于AC的对称点B′,过B′作B′N⊥AB于N,交AC于M.
此时BM+MN的值最小.BM+MN=B′N.
理由:如图1,在AC上任取一点M1(不与点M重合),
在AB上任取一点N1,连接B′M1、BM1、M1N1、B′N1.
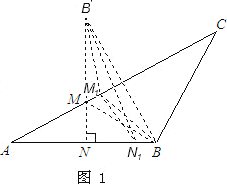
∵点B′与点B关于AC对称,
∴BM1=B′M1,
∴BM1+M1N1=B′M1+M1N1>B′N1.
又∵B′N1>B′N,BM+MN=B′N,
∴BM1+M1N1>BM+MN.
计算:如图2
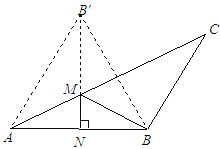
∵点B′与点B关于AC对称,
∴AB′=AB,
又∵∠BAC=30°,
∴∠B′AB=60°,
∴△B′AB是等边三角形.
∴B′B=AB=2,∠B′BN=60°.
又∵B′N⊥AB,
∴B′N=B′Bsin60°=![]() .
.
∴BM+MN的最小值是![]() .
.


科目:初中数学 来源: 题型:
【题目】如图,点B在线段AC上,点E在线段BD上,∠ABD=∠DBC,AB=DB,EB=CB,M,N分别是AE,CD的中点。试探索BM和BN的关系,并证明你的结论。

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,长方形ABCD中,点P沿着边按B→C→D→A方向运动,开始以每秒m个单位匀速运动、a秒后变为每秒2个单位匀速运动,b秒后恢复原速匀速运动,在运动过程中,△ABP的面积S与运动时间t的函数关系如图所示.

(1)直接写出长方形的长和宽;
(2)求m,a,b的值;
(3)当P点在AD边上时,直接写出S与t的函数解析式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD中,AB=AD,点B关于AC的对称点B′ 恰好落在CD上,若∠BAD=110°,则∠ACB的度数为( )

A.40°B.35°C.60°D.70°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】李克强总理说:”一个国家养成全民阅读习惯非常重要…我希望全民阅读能够形成一种氛围,无处不在.“为了响应国家的号召,某”希望“学校的全体师生掀起了阅读的热潮.下面是该校三个年级的学生人数分布扇形统计图与学生在4月份阅读课外书籍人次的统计图表,其中七年级的学生人数为240人.请解答下列问题:
图书种类 | 频数 | 频率 |
科普书籍 | A | B |
文学 | 1200 | C |
漫画丛书 | D | 0.35 |
其他 | 200 | 0.05 |
(1)该校七年级学生人数所在扇形的圆心角为______°,该校的学生总人数为______人;
(2)请补全条形统计图;
(3)为了鼓励学生读书,学校决定在“五四”青年节举行两场读书报告会.报告会的内容从“科普书籍”“文学”“漫画丛书”“其他”中任选两个.用画树状图或列表的方法求两场报告会的内容恰好是“科普书籍”与“漫画丛书”的概率.(“科普书籍”“文学”“漫画丛书”“其他”,可以分别用K,W,M,Q来表示)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,边长相等的两个正方形ABCD和OEFG,若将正方形OEFG绕点O按逆时针方向旋转150°,两个正方形的重叠部分四边形OMCN的面积( )

A. 不变 B. 先增大再减小 C. 先减小再增大 D. 不断增大
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)补充完整:
如图1,在正方形ABCD中,E、F分别为DC、BC边上的点,且满足∠EAF=45°,连结EF,试说明DE+BF=EF.

解:将△ADE绕点A顺时针旋转90°得到△ABG,此时AB与AD重合.由旋转可得AB=AD,GB=ED,∠1=∠2,∠ABG=∠D=90°.
∴∠ABG+∠ABF=90°+90°=180°.
∴点G、B、F在同一条直线上.
∵∠EAF=45°,
∴∠2+∠3=∠BAD-∠EAF=90°-45°=45°
∵∠1=∠2,
∴∠1+∠3=45°.
∴∠GAF=∠ .
又∵AG=AE,AF=AF.
∴△GAF≌ .
∵ =EF.
∴DE+BF=BG+BF=GF=EF.
(2)类比引申:
如图2,在四边形ABCD中,AB=AD,∠BAD=90°,点E、F分别在边BC、CD上,∠EAF=45°,若∠B、∠D都不是直角,则当∠B与∠D满足等量关系 时,有EF=BE+DF.
(3)联想拓展
如图3,在△ABC中,∠BAC=90°,AB=AC,点D、E均在边BC上,且∠DAE=45°,试猜想BD、DE、EC满足的等量关系,并写出推理过程.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠B=90°,AB=6cm,BC=12cm,动点P从点A开始沿边AB向B以1cm/s的速度移动(不与点B重合),动点Q从点B开始沿边BC向C以2cm/s的速度移动(不与点C重合).如果P,Q分别从A,B同时出发,当四边形APQC的面积最小时,经过的时间为( )

A. 1 s B. 2 s C. 3 s D. 4 s
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,D为⊙O上一点,点C在直径BA的延长线上,且∠CDA=∠CBD.
(1)求证:CD是⊙O的切线;
(2)过点B作⊙O的切线交CD的延长线于点E,BC=6, ![]() .求BE的长.
.求BE的长.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com