
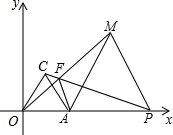
 若P为x轴正半轴上一点,且P在A的右侧,△PAM为等边三角形,OM与PC交于F.求证:AF+MF=PF.
若P为x轴正半轴上一点,且P在A的右侧,△PAM为等边三角形,OM与PC交于F.求证:AF+MF=PF. 分析 将△PAF顺时针旋转60°得到△EAM,得出△PAF≌△MAE,∠FAE=60°,得出PF=EM,AF=AE,证明△EAF是等边三角形,得出EF=AF,即可得出结论.
解答 解:∵△PAM为等边三角形,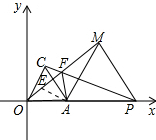
∴AM=AP,
将△PAF顺时针旋转60°得到△EAM,如图所示:
则△PAF≌△MAE,∠FAE=60°,
∴PF=EM,AF=AE,
∴△EAF是等边三角形,
∴EF=AF,
∴AF+MF=EF+MF=EM=PF,
即AF+MF=PF.
点评 本题考查了等边三角形判定与性质、坐标与图形性质、旋转的性质、全等三角形的性质;熟练掌握等边三角形的性质,通过旋转得出等边三角形是解决问题的关键.


科目:初中数学 来源: 题型:解答题
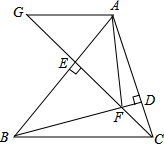 如图.在△ABC中,BD⊥AC于点D,CE⊥AB于点E,BD与CE交于点F,∠BCE=45°
如图.在△ABC中,BD⊥AC于点D,CE⊥AB于点E,BD与CE交于点F,∠BCE=45° 查看答案和解析>>
科目:初中数学 来源: 题型:解答题
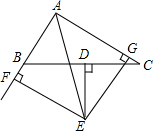 如图,已知△ABC的BC边的垂直平分线DE与∠BAC的平分线交于点E,EF⊥AB的延长线于点F,EG⊥AC于点G,求证:
如图,已知△ABC的BC边的垂直平分线DE与∠BAC的平分线交于点E,EF⊥AB的延长线于点F,EG⊥AC于点G,求证:查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com