
 如图,BD与CE交于点A,AB=AC,AD=AE,△ABC的中线AN的反向延长线交DE于点M,求证:EM=DM.
如图,BD与CE交于点A,AB=AC,AD=AE,△ABC的中线AN的反向延长线交DE于点M,求证:EM=DM. 分析 由等腰三角形的性质证得AG是∠BAC的平分线,然后根据对顶角相等,证明AF是等腰△AED的角平分线,由SAS证明△AME≌△AMD,得出对应边相等即可.
解答 证明:∵△ABC中,AB=AC,AN是中线,
∴AN平分∠BAC,
即∠BAN=∠CAN,
又∵∠EAM=∠CAN,∠DAM=∠BAN,
∴∠EAM=∠DAM,
在△AME和△AMD中,$\left\{\begin{array}{l}{AE=AD}&{\;}\\{∠EAM=∠DAM}&{\;}\\{AM=AM}&{\;}\end{array}\right.$,
∴△AME≌△AMD(SAS),
∴EM=DM.
点评 本题考查了等腰三角形的性质、全等三角形的判定与性质;熟练掌握等腰三角形的性质,证明三角形全等是解决问题的关键.


 名师导航单元期末冲刺100分系列答案
名师导航单元期末冲刺100分系列答案 名校名卷单元同步训练测试题系列答案
名校名卷单元同步训练测试题系列答案科目:初中数学 来源: 题型:选择题
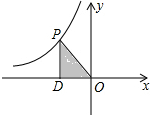 如图,点P是反比例函数y=$\frac{k}{x}$(x<0)图象上一点,过P向x轴作垂线,垂足为D,连接OP.若Rt△POD的面积为2,则k的值为( )
如图,点P是反比例函数y=$\frac{k}{x}$(x<0)图象上一点,过P向x轴作垂线,垂足为D,连接OP.若Rt△POD的面积为2,则k的值为( )| A. | 4 | B. | 2 | C. | -4 | D. | -2 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,直线y=$\frac{4}{3}$x与反比例函数的图象交于点A(3,a),第一象限内的点B在这个反比例函数图象上,OB与x轴正半轴的夹角为α,且tanα=$\frac{1}{3}$.
如图,直线y=$\frac{4}{3}$x与反比例函数的图象交于点A(3,a),第一象限内的点B在这个反比例函数图象上,OB与x轴正半轴的夹角为α,且tanα=$\frac{1}{3}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
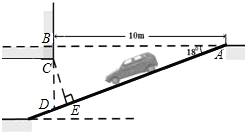 某居民小区为缓解居民停车难问题为缓解“停车难”问题,拟造地下停车库,如图是地下停车库坡道入口的设计示意图,其中,AB⊥BD,∠BAD=18°,C在BD上,BC=0.5.根据规定,地下停车库破道口上方要张贴限高标志,以便告知驾驶员所驾车辆能否安全驶入.请根据以上数据,求出该地下停车库限高CE的长.(结果精确到0.1米)
某居民小区为缓解居民停车难问题为缓解“停车难”问题,拟造地下停车库,如图是地下停车库坡道入口的设计示意图,其中,AB⊥BD,∠BAD=18°,C在BD上,BC=0.5.根据规定,地下停车库破道口上方要张贴限高标志,以便告知驾驶员所驾车辆能否安全驶入.请根据以上数据,求出该地下停车库限高CE的长.(结果精确到0.1米)查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 甲、乙两村与公路AC、BD的相对位置如图所示.现要设立一个医疗站点P,使其满足下列条件:①到公路OA、OB的距离相等;②到甲、乙两村的距离也相等.请确定点P的位置(用直尺和圆规作图,保留作图痕迹).
甲、乙两村与公路AC、BD的相对位置如图所示.现要设立一个医疗站点P,使其满足下列条件:①到公路OA、OB的距离相等;②到甲、乙两村的距离也相等.请确定点P的位置(用直尺和圆规作图,保留作图痕迹).查看答案和解析>>
科目:初中数学 来源: 题型:选择题
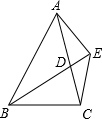 如图,BD为△ABC的角平分线,且BD=BC,E为BD延长线上的一点,BE=BA.则下列结论正确的是:①△ABD≌△EBC;②S△ABD=S△BDC;③∠BCE+∠BCD=180°;④AD=AE=EC;其中正确的是( )
如图,BD为△ABC的角平分线,且BD=BC,E为BD延长线上的一点,BE=BA.则下列结论正确的是:①△ABD≌△EBC;②S△ABD=S△BDC;③∠BCE+∠BCD=180°;④AD=AE=EC;其中正确的是( )| A. | ①②③ | B. | ①③④ | C. | ①②④ | D. | ①②③④ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
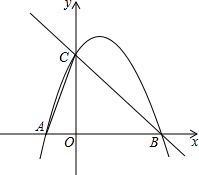 如图,己知抛物线与x轴分别交于A(-1,0)、B(3,0)两点,与y轴交于点C(0,3).
如图,己知抛物线与x轴分别交于A(-1,0)、B(3,0)两点,与y轴交于点C(0,3).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com