
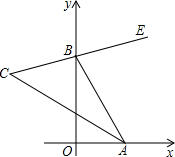
 已知如图∠xOy=90°,BE是∠ABy的平分线,BE的反向延长线与∠OAB的平分线相交于点C,当点A,B分别在射线Ox,Oy上移动时,试问∠ACB的大小是否发生变化?如果保持不变,请说明理由;如果随点A,B的移动而变化,请求出变化范围.
已知如图∠xOy=90°,BE是∠ABy的平分线,BE的反向延长线与∠OAB的平分线相交于点C,当点A,B分别在射线Ox,Oy上移动时,试问∠ACB的大小是否发生变化?如果保持不变,请说明理由;如果随点A,B的移动而变化,请求出变化范围. 科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
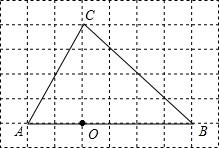 如图,在6×8的网格图中,每个小正方形边长均为1,点O和△ABC的顶点均为小正方形的顶点.以O为位似中心,在网格图中作△A′B′C′,使△A′B′C′和△ABC位似,且位似比为1:2.
如图,在6×8的网格图中,每个小正方形边长均为1,点O和△ABC的顶点均为小正方形的顶点.以O为位似中心,在网格图中作△A′B′C′,使△A′B′C′和△ABC位似,且位似比为1:2.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
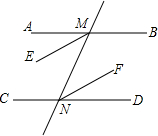 如图,已知直线AB∥CD,直线MN分别交AB、CD于M、N两点,若ME、NF分别是∠AMN、∠DNM的角平分线,试说明:ME∥NF.
如图,已知直线AB∥CD,直线MN分别交AB、CD于M、N两点,若ME、NF分别是∠AMN、∠DNM的角平分线,试说明:ME∥NF.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
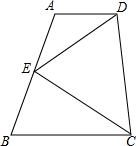 如图,在梯形ABCD中,AD∥BC,E是AB的中点.
如图,在梯形ABCD中,AD∥BC,E是AB的中点.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com