
分析 (1)根据方向角的定义及已知条件即可画出示意图;
(2)过点C作CD⊥AB于D,由题意知道∠DAC=31°,∠DBC=45°,设CD=x米,则AD=AB+BD=(20+x)米,在Rt△ACD中,tan∠DAC=$\frac{CD}{AD}$,由此可以列出关于x的方程,解方程即可求解.
解答 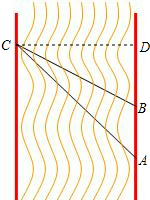 解:(1)如图所示:
解:(1)如图所示:
(2)过点C作CD⊥AB,垂足为D,设CD=x米,
∵在Rt△BCD中,∠CBD=45°,
∴BD=CD=x米.
在Rt△ACD中,∠DAC=31°,
AD=AB+BD=(20+x)米,CD=x米,
∵tan∠DAC=$\frac{CD}{AD}$,
∴$\frac{x}{20+x}$=$\frac{3}{5}$,
解得x=30.
经检验x=30是原方程的解,且符合题意.
答:这条河的宽度为30米.
点评 此题主要考查了解直角三角形-方向角问题,解题时首先正确理解题意,然后根据题目隐含的数量关系列出方程解决问题.


科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
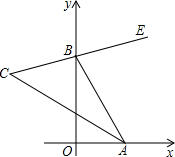 已知如图∠xOy=90°,BE是∠ABy的平分线,BE的反向延长线与∠OAB的平分线相交于点C,当点A,B分别在射线Ox,Oy上移动时,试问∠ACB的大小是否发生变化?如果保持不变,请说明理由;如果随点A,B的移动而变化,请求出变化范围.
已知如图∠xOy=90°,BE是∠ABy的平分线,BE的反向延长线与∠OAB的平分线相交于点C,当点A,B分别在射线Ox,Oy上移动时,试问∠ACB的大小是否发生变化?如果保持不变,请说明理由;如果随点A,B的移动而变化,请求出变化范围.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 等于5cm | B. | 等于6cm | C. | 等于4cm | D. | 小于或等于4cm |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com