练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】如图，将Rt△ABC绕直角顶点C顺时针旋转90°，得到△A′B′C′，连接AA′，若∠1=27°，则∠B的度数是（ ）
    A.84°
    B.72°
    C.63°
    D.54°

    【答案】B
    【解析】解：∵Rt△ABC绕直角顶点C顺时针旋转90°得到△A′B′C， ∴AC=A′C，
    ∴△ACA′是等腰直角三角形，
    ∴∠CAA′=45°，
    ∴∠A′B′C=∠1+∠CAA′=27°+45°=72°，
    由旋转的性质得：∠B=∠A′B′C=72°．
    故选：B．
    根据旋转的性质可得AC=A′C，然后判断出△ACA′是等腰直角三角形，根据等腰直角三角形的性质可得∠CAA′=45°，再根据三角形的外角性质求出∠A′B′C，然后根据旋转的性质可得∠B=∠A′B′C．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】（8分）如图，一次函数（）的图象经过点C（3，0），且与两坐标轴围成的三角形的面积为3．

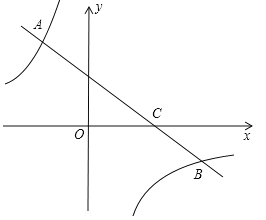
    （1）求该一次函数的解析式；

    （2）若反比例函数的图象与该一次函数的图象交于二、四象限内的A、B两点，且AC=2BC，求m的值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】钓鱼岛自古就是中国领土，中国政府已对钓鱼岛开展常态化巡逻.某天，为按计划准点到达指定海域，某巡逻艇凌晨1：00出发，匀速行驶一段时间后，因中途出现故障耽搁了一段时间，故障排除后，该艇加快速度仍匀速前进，结果恰好准点到达.如图是该艇行驶的路程（海里）与所用时间t（小时）的函数图象，则该巡逻艇原计划准点到达的时刻是 .

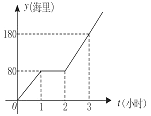
    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】关于x的一元二次方程（a﹣1）x2+x+a2﹣1=0的一个根是0，则a的值是（ ）
    A.﹣1
    B.1
    C.1或﹣1
    D.﹣1或0

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】下面是小林画出函数 的一部分图象，利用图象回答：

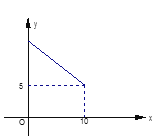
    （1）自变量x的取值范围.
    （2）当x取什么值时，y的最小值.最大值各是多少？
    （3）在图中，当x增大时，y的值是怎样变化？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，已知△ABC各顶点的坐标分别为A（﹣2，5）B（﹣5，﹣2），C（3，3）．将△ABC先向右平移4个单位长度，再向下平移3个单位长度，得到△A′B′C′．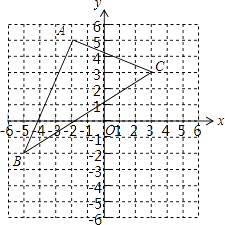
    （1）在图中画出第二次平移之后的图形△A′B′C′；
    （2）如果将△A′B′C′看成是由△ABC经过一次平移得到的，请指出这一平移的平移方向和平移距离．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在平面直角坐标系xOy中，△ABC三个顶点的坐标分别为A（﹣5，1），B（﹣4，4），C（﹣1，﹣1）．将△ABC向右平移5个单位长度，再向下平移4个单位长度，得到△A′B′C′，其中点A′，B′，C′分别为点A，B，C的对应点．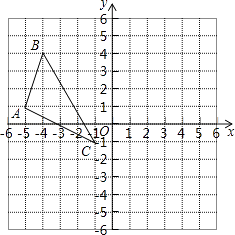
    （1）请在所给坐标系中画出△A′B′C′，并直接写出点C′的坐标；
    （2）若AB边上一点P经过上述平移后的对应点为P′（x，y），用含x，y的式子表示点P的坐标．（直接写出结果即可）

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图1，点P是线段AB上的动点（P不与A、B重合），分别以AP、BP为边向线段AB的同侧作等边△APC和等边△BPD，AD和BC交于点M．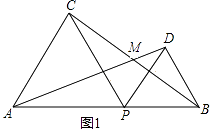
    （1）求证：AD=BC；
    （2）将点P在线段AB上随意固定，再把△BPD按顺时针方向绕点P旋转一个角度α（α＜60°），如图2所示，在旋转过程中，∠AMC的度数是否与α的大小有关？证明你的结论．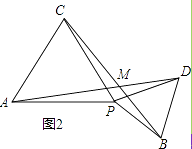

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】若－2xm＋1＋7yn＋3＝8是关于x，y的二元一次方程，则m＝________，n＝________．

    查看答案和解析>>

    同步练习册答案