
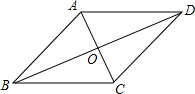
 如图,平行四边形ABCD中,对角线AC、BD相交于点O,现从以下四个式子①AB=BC,②AC=BD,③AC⊥BD,④∠ABC=90°中,任取一个作为条件,即可推出平行四边形ABCD是菱形的概率为$\frac{1}{2}$.
如图,平行四边形ABCD中,对角线AC、BD相交于点O,现从以下四个式子①AB=BC,②AC=BD,③AC⊥BD,④∠ABC=90°中,任取一个作为条件,即可推出平行四边形ABCD是菱形的概率为$\frac{1}{2}$. 分析 由菱形的判定定理“有一组邻边相等的平行四边形是菱形”和“对角线互相垂直的平行四边形是菱形”对四个选项进行逐一判断,找出正确的条件个数,再根据概率公式即可解答.
解答  解:四边形ABCD是平行四边形,
解:四边形ABCD是平行四边形,
(1)若AB=BC,则AB=BC=CD=AD,符合“有一组邻边相等的平行四边形是菱形”的判定定理,故此小题正确;
(2)若AC=BD,则此平行四边形是矩形,故此小题错误;
(3)若AC⊥BD,符合“对角线互相垂直的平行四边形是菱形”的判定定理,此小题正确;
(4)若AB⊥BC,则此平行四边形是矩形,故此小题错误.
故正确的有(1)、(3)两个,
所以可推出平行四边形ABCD是菱形的概率为:$\frac{2}{4}$=$\frac{1}{2}$.
故答案为:$\frac{1}{2}$.
点评 本题考查的是概率公式及菱形的判定定理,解答此题的关键是熟知概率的求法与运用,一般方法:如果一个事件有n种可能,而且这些事件的可能性相同,其中事件A出现m种结果,那么事件A的概率P(A)=$\frac{m}{n}$.


科目:初中数学 来源: 题型:选择题
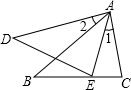 如图,已知∠1=∠2,那么添加下列一个条件后,仍无法判定△ABC∽△ADE的是( )
如图,已知∠1=∠2,那么添加下列一个条件后,仍无法判定△ABC∽△ADE的是( )| A. | ∠C=∠AED | B. | $\frac{AB}{AD}=\frac{AC}{AE}$ | C. | ∠B=∠D | D. | $\frac{AB}{AD}=\frac{BC}{DE}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | ax2-a=a(x2-1) | B. | x2+x-2=x(x+1)-2 | C. | a2b+ab2=ab(a+b) | D. | x2+1=x(x+$\frac{1}{x}$) |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | ①② | B. | ①③ | C. | ①②④ | D. | ①③④ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 图中线段AB表示某工程的部分隧道,无人勘测飞机从隧道的一侧点A出发,沿着坡度为1:1.5的路线AE飞行,飞行至分界点C的正上方点D时,测得隧道另一侧点B的俯角为23°,继续飞行至点E,测得点B的俯角为45°,此时点E离地面的高度EF=800米.
图中线段AB表示某工程的部分隧道,无人勘测飞机从隧道的一侧点A出发,沿着坡度为1:1.5的路线AE飞行,飞行至分界点C的正上方点D时,测得隧道另一侧点B的俯角为23°,继续飞行至点E,测得点B的俯角为45°,此时点E离地面的高度EF=800米.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com