
 图中线段AB表示某工程的部分隧道,无人勘测飞机从隧道的一侧点A出发,沿着坡度为1:1.5的路线AE飞行,飞行至分界点C的正上方点D时,测得隧道另一侧点B的俯角为23°,继续飞行至点E,测得点B的俯角为45°,此时点E离地面的高度EF=800米.
图中线段AB表示某工程的部分隧道,无人勘测飞机从隧道的一侧点A出发,沿着坡度为1:1.5的路线AE飞行,飞行至分界点C的正上方点D时,测得隧道另一侧点B的俯角为23°,继续飞行至点E,测得点B的俯角为45°,此时点E离地面的高度EF=800米.分析 (1)要求AC和BC的长度,只要求出AB的长度,根据坡度为1:1.5,EF的长度为800米,可以求得AF的长度,AC与CD的关系,根据点B的俯角为45°,可以求得BF的长度,从而可以求得AB的长度,进而求得隧道AC和BC段的长度;
(2)根据题意可以知道原计划甲、乙两队工作效率的关系,然后根据两队同时开工5天后,甲队将速度提高25%,乙队将速度提高了150%,从而两队同时完成,可以列出相应的方程组,从而可以解答本题.
解答 解:(1)由题意可得,
tan∠A=$\frac{1}{1.5}=\frac{2}{3}$,∠DBC=23°,∠EBF=45°,
∵$tan∠A=\frac{CD}{AC}=\frac{EF}{AF}$,EF=800,∠EFB=90°,∠EBF=45°,
∴AF=1200,设CD=2x,则AC=3x,BF=800,
∴AB=AF+BF=1200+800=2000,
∵$tan∠DBC=\frac{CD}{BC}=\frac{2x}{2000-3x}$,∠DBC=23°,
解得,x=250
∴3x=750,BC=2000-750=1250,
即隧道AC的长度是750米,BC段的长度是1250米;
(2)设原计划甲队每天施工x米,乙队每天施工y米,
$\left\{\begin{array}{l}{y=2x}\\{\frac{750-5x}{x(1+25%)}=\frac{1250-5y}{y(1+150%)}}\end{array}\right.$
解得$\left\{\begin{array}{l}{x=175}\\{y=350}\end{array}\right.$,
即原计划甲队每天施工175米,乙队每天施工350米.
点评 本题考查解直角三角形的应用--坡度坡角问题、分式方程的应用,解题的关键是明确题意,找出题目中的数量关系,列出相应的方程组并解答.


 激活思维优加课堂系列答案
激活思维优加课堂系列答案 活力试卷系列答案
活力试卷系列答案科目:初中数学 来源: 题型:填空题
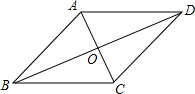 如图,平行四边形ABCD中,对角线AC、BD相交于点O,现从以下四个式子①AB=BC,②AC=BD,③AC⊥BD,④∠ABC=90°中,任取一个作为条件,即可推出平行四边形ABCD是菱形的概率为$\frac{1}{2}$.
如图,平行四边形ABCD中,对角线AC、BD相交于点O,现从以下四个式子①AB=BC,②AC=BD,③AC⊥BD,④∠ABC=90°中,任取一个作为条件,即可推出平行四边形ABCD是菱形的概率为$\frac{1}{2}$.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 浙江卫视“奔跑吧兄弟”综艺节目的收视率,采用抽查的方式 | |
| B. | 了解某渔场中青鱼的平均重量,采用抽查的方式 | |
| C. | 了解iPhone6s手机的使用寿命,采用普查的方式 | |
| D. | 了解一批汽车的刹车性能,采用普查的方式 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com