
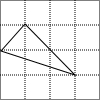
 某同学在方格纸上画了四个三角形,与书本上的三角形(如图)相似的是( )
某同学在方格纸上画了四个三角形,与书本上的三角形(如图)相似的是( )| A. |  | B. | 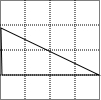 | C. | 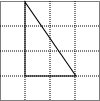 | D. | 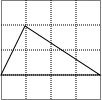 |
分析 先根据勾股定理得出题中给出的三角形的边长,再求出各选项中三角形的边长,根据相似三角形的判定定理即可得出结论.
解答 解:图中三角形三边长分别为:$\sqrt{{1}^{2}+{1}^{2}}$=$\sqrt{2}$,$\sqrt{{1}^{2}+{3}^{2}}$=$\sqrt{10}$,$\sqrt{{2}^{2}+{2}^{2}}$=$\sqrt{8}$.
A、图中三角形三边长分别为2,$\sqrt{{1}^{2}+{3}^{2}}$=$\sqrt{10}$,$\sqrt{{3}^{2}+{3}^{2}}$=$\sqrt{18}$与原三角形的三边不成比例,故本选项错误;
B、图中三角形三边长分别为2,4,$\sqrt{{4}^{2}+{2}^{2}}$=$\sqrt{20}$,
∵$\frac{\sqrt{2}}{2}$=$\frac{\sqrt{8}}{4}$=$\frac{\sqrt{10}}{\sqrt{20}}$与原三角形的三边成比例,∴与书本上的三角形(如图)相似,故本选项正确;
C、图中三角形三边长分别为2,3,$\sqrt{{2}^{2}+{2}^{2}}$=$\sqrt{8}$与原三角形的三边不成比例,故本选项错误
D、图中三角形三边长分别为$\sqrt{{1}^{2}+{2}^{2}}$=$\sqrt{5}$,$\sqrt{{2}^{2}+{3}^{2}}$=$\sqrt{13}$,4与原三角形的三边不成比例,故本选项错误.
故选B.
点评 本题考查的是相似三角形的判定定理,熟知三组对应边的比相等的两个三角形相似是解答此题的关键.


 鸿图图书寒假作业假期作业吉林大学出版社系列答案
鸿图图书寒假作业假期作业吉林大学出版社系列答案科目:初中数学 来源: 题型:解答题
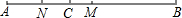
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 图中线段AB表示某工程的部分隧道,无人勘测飞机从隧道的一侧点A出发,沿着坡度为1:1.5的路线AE飞行,飞行至分界点C的正上方点D时,测得隧道另一侧点B的俯角为23°,继续飞行至点E,测得点B的俯角为45°,此时点E离地面的高度EF=800米.
图中线段AB表示某工程的部分隧道,无人勘测飞机从隧道的一侧点A出发,沿着坡度为1:1.5的路线AE飞行,飞行至分界点C的正上方点D时,测得隧道另一侧点B的俯角为23°,继续飞行至点E,测得点B的俯角为45°,此时点E离地面的高度EF=800米.查看答案和解析>>
科目:初中数学 来源: 题型:解答题

| n | an | n | an |
| 1 | 3 | 2 | 6 |
| 3 | 8 | 4 | 11 |
| 5 | 13 | 6 | 16 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
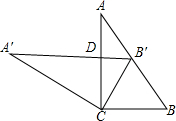 如图,将两块大小相同的三角板重叠在一起,∠A=30°,∠B=60°,BC=10cm,把上面一块三角板绕顶点C作逆时针方向旋转到△A′B′C′的位置,点B′在AB上,A′B′与AC相交于点D,则A′D的长度为( )
如图,将两块大小相同的三角板重叠在一起,∠A=30°,∠B=60°,BC=10cm,把上面一块三角板绕顶点C作逆时针方向旋转到△A′B′C′的位置,点B′在AB上,A′B′与AC相交于点D,则A′D的长度为( )| A. | 14cm | B. | 15cm | C. | 16cm | D. | 17cm |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com