

| n | an | n | an |
| 1 | 3 | 2 | 6 |
| 3 | 8 | 4 | 11 |
| 5 | 13 | 6 | 16 |
分析 (1)根据图形的变化,可知偶数下标比前一个图形多3根,奇数下标比前一个图形多2根,套入数据即可得出结论;
(2)根据图形的变化,可知偶数下标比前一个图形多3根,奇数下标比前一个图形多2根,将n分奇偶处理,看1到n中有多少个偶数和奇数,从而得出结论;
(3)令an=2016,an=2015,套用(2)得出的结果即可结论.
解答 解:根据图形的变化,可知图2比图1多3根火柴棒,图3比图2多2根火材棒,图4比图3多3根火柴棒…,即多的数目3、2交替.
(1)a3=a2+2=6+2=8,a4=a3+3=8+3=11,a5=a4+2=11+2=13,a6=a5+3=13+3=16.
故答案为:8;11;13;16.
(2)a1=3=1+2.
当n为奇数时,1到n中有$\frac{n-1}{2}$个偶数,有$\frac{n+1}{2}$个奇数,
结合发现的规律可知:an=1+$\frac{n+1}{2}$×2+$\frac{n-1}{2}$×3=$\frac{5n+1}{2}$,
故小亮说的正确.
当n为偶数时,1到n中有$\frac{n}{2}$个偶数,有$\frac{n}{2}$个奇数,
结合发现的规律可知:an=1+$\frac{n}{2}$×2+$\frac{n}{2}$×3=$\frac{5n+2}{2}$.
(3)令an=2016,即$\frac{5n+1}{2}$=2016,或$\frac{5n+2}{2}$=2016,
解得:n=$\frac{4031}{5}$,或n=806;
令an=2015,即$\frac{5n+1}{2}$=2015,或$\frac{5n+2}{2}$=2015,
解得:n=$\frac{4029}{5}$,或n=$\frac{4028}{5}$.
综上可知,an能取2016,此时n的值为806.
点评 本题考查了图形的变化,解题的关键是:发现“偶数下标比前一个图形多3根,奇数下标比前一个图形多2根”.本题属于中档题型,有点难度,难点再与如何去寻找规律,做形如此类题型时,不妨将数据分成奇偶两组来讨论.


科目:初中数学 来源: 题型:选择题
| A. | y3-y=y(y2-1) | B. | x2-x-3=x(x-1)-3 | C. | -m2+n2=-(m-n)(m+n) | D. | x2-3x+9=(x-3)2 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
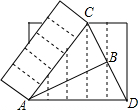 两张一边长相等的长方形纸片(AC=AD)如图放置,重合的顶点记为A,现将它们都分成5个宽度相等的长方形,点C是其中一条分割线与边的交点,连结CD与分割线交于点B,若AD=5,则△ABC的面积是5.
两张一边长相等的长方形纸片(AC=AD)如图放置,重合的顶点记为A,现将它们都分成5个宽度相等的长方形,点C是其中一条分割线与边的交点,连结CD与分割线交于点B,若AD=5,则△ABC的面积是5.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
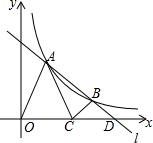 如图,直线l与双曲线$y=\frac{k}{x}$的一支相交于A、B两点,l与x轴相交于点D,C为线段OD中点,△OAC与△BCD分别是以OC、CD为底的等腰三角形,且S△OAC+S△BCD=2,则k=$\frac{3}{2}$.
如图,直线l与双曲线$y=\frac{k}{x}$的一支相交于A、B两点,l与x轴相交于点D,C为线段OD中点,△OAC与△BCD分别是以OC、CD为底的等腰三角形,且S△OAC+S△BCD=2,则k=$\frac{3}{2}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
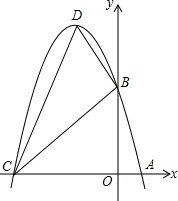 如图,抛物线y=-x2+bx+c与x轴交于点A、C,与y轴交于点B,它的顶点是D,对称轴是直线x=-2,且OB=OC.
如图,抛物线y=-x2+bx+c与x轴交于点A、C,与y轴交于点B,它的顶点是D,对称轴是直线x=-2,且OB=OC.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com