
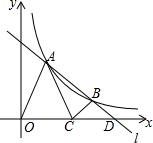
 如图,直线l与双曲线$y=\frac{k}{x}$的一支相交于A、B两点,l与x轴相交于点D,C为线段OD中点,△OAC与△BCD分别是以OC、CD为底的等腰三角形,且S△OAC+S△BCD=2,则k=$\frac{3}{2}$.
如图,直线l与双曲线$y=\frac{k}{x}$的一支相交于A、B两点,l与x轴相交于点D,C为线段OD中点,△OAC与△BCD分别是以OC、CD为底的等腰三角形,且S△OAC+S△BCD=2,则k=$\frac{3}{2}$. 分析 作AE⊥x轴于点E,作BF⊥x轴于点F,则△BDF∽△ADE,设A的横坐标是m,纵坐标是n,则mn=k,B坐标可以利用m、n表示,则利用m和n表示出△OAC和△BCD的面积,然后根据S△OAC+S△BCD=2,得到一个关于k的方程,从而求解.
解答  解:作AE⊥x轴于点E,作BF⊥x轴于点F.
解:作AE⊥x轴于点E,作BF⊥x轴于点F.
∵AO=AC,BC=BD,
∴OE=EC,CF=FD,
又∵OC=CD,
∴OE=EC=CF=FD.
∵AE⊥x,BF⊥x,
∴AE∥BF,
∴△BDF∽△ADE,
∴$\frac{BF}{AE}$=$\frac{FD}{DE}$=$\frac{1}{3}$,即BF=$\frac{1}{3}$AE.
设A的横坐标是m,纵坐标是n,则mn=k,B的横坐标3m,纵坐标是$\frac{1}{3}$n.
则S△OAC=$\frac{1}{2}$×2mn=mn=k.S△BCD=$\frac{1}{2}$×2m×$\frac{1}{3}$n=$\frac{1}{3}$mn=$\frac{1}{3}$k.
∵S△OAC+S△BCD=2,
∴k+$\frac{1}{3}$k=2,
解得:k=$\frac{3}{2}$.
故答案是:$\frac{3}{2}$.
点评 本题考查了等腰三角形的性质以及相似三角形的判定与性质,利用k表示出△OAC和△BCD的面积是关键.


科目:初中数学 来源: 题型:解答题
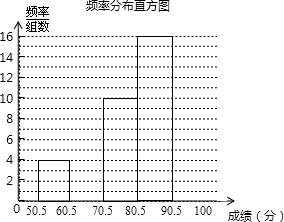 6月5日是世界环保日.为了让学生了解环保知识,某中学组织全校2000名学生参加了“环保知识竞赛”.为了解本次竞赛成绩的分布情况,从中抽取了部分学生的成绩(满分100分,得分均为正整数)进行统计,得到下面的频率分布表和频数分布直方图.
6月5日是世界环保日.为了让学生了解环保知识,某中学组织全校2000名学生参加了“环保知识竞赛”.为了解本次竞赛成绩的分布情况,从中抽取了部分学生的成绩(满分100分,得分均为正整数)进行统计,得到下面的频率分布表和频数分布直方图.| 分数段 | 频数 | 频率 |
| 50.5-60.5 | 4 | 0.08 |
| 60.5-70.5 | 8 | 0.16 |
| 70.5-80.5 | 10 | 0.20 |
| 80.5-90.5 | 16 | 0.32 |
| 90.5-100.5 | 12 | 0.24 |
| 合计 | 1 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

| n | an | n | an |
| 1 | 3 | 2 | 6 |
| 3 | 8 | 4 | 11 |
| 5 | 13 | 6 | 16 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
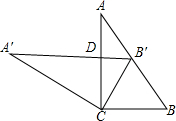 如图,将两块大小相同的三角板重叠在一起,∠A=30°,∠B=60°,BC=10cm,把上面一块三角板绕顶点C作逆时针方向旋转到△A′B′C′的位置,点B′在AB上,A′B′与AC相交于点D,则A′D的长度为( )
如图,将两块大小相同的三角板重叠在一起,∠A=30°,∠B=60°,BC=10cm,把上面一块三角板绕顶点C作逆时针方向旋转到△A′B′C′的位置,点B′在AB上,A′B′与AC相交于点D,则A′D的长度为( )| A. | 14cm | B. | 15cm | C. | 16cm | D. | 17cm |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
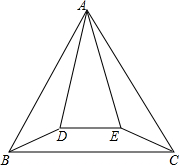 如图,正△ABC与等腰△ADE的顶点A重合,AD=AE,∠DAE=30°,将△ADE绕顶点A旋转,在旋转过程中,当BD=CE时,∠BAD的大小可以是15°或165°.
如图,正△ABC与等腰△ADE的顶点A重合,AD=AE,∠DAE=30°,将△ADE绕顶点A旋转,在旋转过程中,当BD=CE时,∠BAD的大小可以是15°或165°.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com