
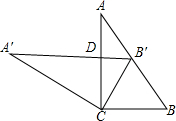
 如图,将两块大小相同的三角板重叠在一起,∠A=30°,∠B=60°,BC=10cm,把上面一块三角板绕顶点C作逆时针方向旋转到△A′B′C′的位置,点B′在AB上,A′B′与AC相交于点D,则A′D的长度为( )
如图,将两块大小相同的三角板重叠在一起,∠A=30°,∠B=60°,BC=10cm,把上面一块三角板绕顶点C作逆时针方向旋转到△A′B′C′的位置,点B′在AB上,A′B′与AC相交于点D,则A′D的长度为( )| A. | 14cm | B. | 15cm | C. | 16cm | D. | 17cm |
分析 首先证明△BCB′是等边三角形、A′B′∥BC,得∠A′DC=∠ACB=90°,在RT△ABC中求出AC,根据A′C=AC,再在Rt△A′DC中利用勾股定理即可求出A′D.
解答  解:∵△A′B′C是由△ABC旋转,
解:∵△A′B′C是由△ABC旋转,
∴BC=CB′,
∵∠B=60°,
∴△BCB′是等边三角形,
∴∠BCB′=60°,
∵∠A′B′C=60°,
∴∠A′B′C=∠BCB′,
∴A′B′∥BC,
∴∠A′DC=∠ACB=90°,
∵∠A′CB′=∠ACB=90°,
∴∠A′CD=∠BCB′=60°,
∴∠A′=30°,
在Rt△ACB中,∵BC=10,∠B=60°,
∴∠A=30°,AB=2BC=20,AC=$\sqrt{A{B}^{2}-B{C}^{2}}$=10$\sqrt{3}$,
在Rt△A′CD中,∵∠A′=30°,A′C=AC=10$\sqrt{3}$,
∴CD=$\frac{1}{2}$A′C=5$\sqrt{3}$,A′D=$\sqrt{A′{C}^{2}-C{D}^{2}}$=$\sqrt{(10\sqrt{3})^{2}-(5\sqrt{3})^{2}}$=15.
故选B.
点评 本题考查旋转的性质、勾股定理、等边三角形的判定和性质、解题的关键是利用特殊图形解决问题,解题时要充分利用旋转不变性,属于中考常考题型.


 一诺书业暑假作业快乐假期云南美术出版社系列答案
一诺书业暑假作业快乐假期云南美术出版社系列答案科目:初中数学 来源: 题型:填空题
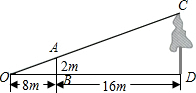 如图,为了测量校园内某棵树的高度,张敏用长为2m的竹竿做测量工具,移动竹竿,使竹竿、树的顶端的影子恰好落在地面的同一点O处.此时,竹竿与O点相距8m,竹竿与树相距16m,则树的高度为6m.
如图,为了测量校园内某棵树的高度,张敏用长为2m的竹竿做测量工具,移动竹竿,使竹竿、树的顶端的影子恰好落在地面的同一点O处.此时,竹竿与O点相距8m,竹竿与树相距16m,则树的高度为6m.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
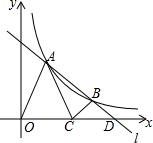 如图,直线l与双曲线$y=\frac{k}{x}$的一支相交于A、B两点,l与x轴相交于点D,C为线段OD中点,△OAC与△BCD分别是以OC、CD为底的等腰三角形,且S△OAC+S△BCD=2,则k=$\frac{3}{2}$.
如图,直线l与双曲线$y=\frac{k}{x}$的一支相交于A、B两点,l与x轴相交于点D,C为线段OD中点,△OAC与△BCD分别是以OC、CD为底的等腰三角形,且S△OAC+S△BCD=2,则k=$\frac{3}{2}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com