
分析 首先把x=2-$\sqrt{5}$代入x2-4x+c=0可得c的值,然后再根据韦达定理可得x1+x2=4,x1x2=-1,把(x1-x2)2变形为(x1+x2)2-4x1x2,再代入求值即可.
解答 解:由题意得:(2-$\sqrt{5}$)2-4(2-$\sqrt{5}$)+c=0,
解得:c=-1,
把c=-1代入x2-4x+c=0可得:x2-4x-1=0,
∵a=1,b=-4,c=-1,
∴x1+x2=4,x1x2=-1,
(x1-x2)2=(x1+x2)2-4x1x2=42-4×(-1)=20.
点评 此题主要考查了根与系数的关系,以及一元二次方程的解,关键是掌握x1,x2是一元二次方程ax2+bx+c=0(a≠0)的两根时,x1+x2=$\frac{b}{a}$,x1x2=$\frac{c}{a}$.


 学期复习一本通学习总动员期末加暑假延边人民出版社系列答案
学期复习一本通学习总动员期末加暑假延边人民出版社系列答案 芒果教辅暑假天地重庆出版社系列答案
芒果教辅暑假天地重庆出版社系列答案科目:初中数学 来源: 题型:解答题
 图中线段AB表示某工程的部分隧道,无人勘测飞机从隧道的一侧点A出发,沿着坡度为1:1.5的路线AE飞行,飞行至分界点C的正上方点D时,测得隧道另一侧点B的俯角为23°,继续飞行至点E,测得点B的俯角为45°,此时点E离地面的高度EF=800米.
图中线段AB表示某工程的部分隧道,无人勘测飞机从隧道的一侧点A出发,沿着坡度为1:1.5的路线AE飞行,飞行至分界点C的正上方点D时,测得隧道另一侧点B的俯角为23°,继续飞行至点E,测得点B的俯角为45°,此时点E离地面的高度EF=800米.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
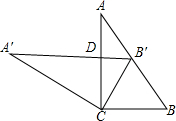 如图,将两块大小相同的三角板重叠在一起,∠A=30°,∠B=60°,BC=10cm,把上面一块三角板绕顶点C作逆时针方向旋转到△A′B′C′的位置,点B′在AB上,A′B′与AC相交于点D,则A′D的长度为( )
如图,将两块大小相同的三角板重叠在一起,∠A=30°,∠B=60°,BC=10cm,把上面一块三角板绕顶点C作逆时针方向旋转到△A′B′C′的位置,点B′在AB上,A′B′与AC相交于点D,则A′D的长度为( )| A. | 14cm | B. | 15cm | C. | 16cm | D. | 17cm |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,△ABC中,AB=AC,以AC为直径的⊙O交AB于点M,交BC于点N,连接AN,过点C作⊙O的切线,交AB的延长线于点P.
如图,△ABC中,AB=AC,以AC为直径的⊙O交AB于点M,交BC于点N,连接AN,过点C作⊙O的切线,交AB的延长线于点P.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com