
分析 (1)设买A种毛笔x元,根据题意可得到一个一元一次不等式,解不等式可得到最多能购买A种毛笔的数量;
(2)根据“购买B种毛笔的数量要小于A种毛笔数量的2倍”可得出x的范围,再根据一次函数的增减性,即可求得最少花费.
解答 解:(1)设能买A种毛笔x本,则能买B种毛笔(40-x)本,
根据题意,得 15x+10(40-x)≤500,
解得:x≤20.
答:最多能购买A种毛笔20支;
(2)设购买A,B两种毛笔共花费W元,则:W=15x+10(40-x)=5x+400,
由题意,得:40-x<2x,
解得:x>$\frac{40}{3}$,
∵k=5>0.w随x的增大而增大,当x取最小时,花费最少,
又∵x>$\frac{40}{3}$,x为整数,
∴当x=14时,W最小=5×14+400=470(元).
答:购买A种笔记本14本,B种笔记本26本时,花费最少,此时的花费是470元.
点评 此题考查了一次函数的应用,解题关键是要读懂题目的意思,根据题目给出的条件,将实际问题转化为一次函数的知识进行求解,难度一般.


 同步练习强化拓展系列答案
同步练习强化拓展系列答案科目:初中数学 来源: 题型:解答题

| n | an | n | an |
| 1 | 3 | 2 | 6 |
| 3 | 8 | 4 | 11 |
| 5 | 13 | 6 | 16 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
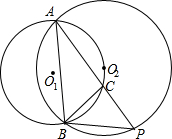 如图,⊙O1与⊙O2都经过A、B两点,且点O2在⊙O1上,点C是弧A O2B上的一动点(点C不与点A、B重合),连接AC并延长AC交O2点P,连接AB,BC,BP,无论点C怎样移动,(1)∠BAP (2)∠APB (3)∠ABC(4)∠ACB(5)∠PBC(6)∠PCB中,大小都不变的角是(2)(4)(5)(6)(填写序号)
如图,⊙O1与⊙O2都经过A、B两点,且点O2在⊙O1上,点C是弧A O2B上的一动点(点C不与点A、B重合),连接AC并延长AC交O2点P,连接AB,BC,BP,无论点C怎样移动,(1)∠BAP (2)∠APB (3)∠ABC(4)∠ACB(5)∠PBC(6)∠PCB中,大小都不变的角是(2)(4)(5)(6)(填写序号)查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com