
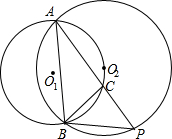
 如图,⊙O1与⊙O2都经过A、B两点,且点O2在⊙O1上,点C是弧A O2B上的一动点(点C不与点A、B重合),连接AC并延长AC交O2点P,连接AB,BC,BP,无论点C怎样移动,(1)∠BAP (2)∠APB (3)∠ABC(4)∠ACB(5)∠PBC(6)∠PCB中,大小都不变的角是(2)(4)(5)(6)(填写序号)
如图,⊙O1与⊙O2都经过A、B两点,且点O2在⊙O1上,点C是弧A O2B上的一动点(点C不与点A、B重合),连接AC并延长AC交O2点P,连接AB,BC,BP,无论点C怎样移动,(1)∠BAP (2)∠APB (3)∠ABC(4)∠ACB(5)∠PBC(6)∠PCB中,大小都不变的角是(2)(4)(5)(6)(填写序号) 分析 根据同弧所对的圆周角相等得∠APB=∠AP′B,∠ACB=∠AC′B,再根据补角的定义得∠BCP=∠BC′P′,根据三角形内角和定理可知∠PBC=∠P′BC′由此即可解决问题.
解答 解:如图 ,点C′是弧A O2B上的一点,延长AC′交⊙O2于P′,连接BP′,
,点C′是弧A O2B上的一点,延长AC′交⊙O2于P′,连接BP′,
∵∠APB=∠AP′B
∴∠APB不变,故(2)不变
∵∠ACB=∠AC′B,
∴∠ACB不变,故(4)不变,
∵∠BCP=180°-∠ACB,∠BC′P=180°-∠AC′B,
∴∠BCP=∠BC′P,
∴∠BCP不变,故(6)不变,
∵∠PBC=180°-∠APB-∠BCP,∠P′BC′=180°-∠AP′B-∠BC′P′,
∴∠PBC=∠P′BC′,故(5)不变,
故答案为(2)(4)(5)(6).
点评 本题考查相交两圆的性质、三角形内角和定理等知识,利用同弧所对的圆周角相等是解决问题的关键,学会添加辅助线,证明类似问题.


 孟建平小学滚动测试系列答案
孟建平小学滚动测试系列答案 黄冈天天练口算题卡系列答案
黄冈天天练口算题卡系列答案科目:初中数学 来源: 题型:解答题
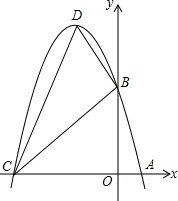 如图,抛物线y=-x2+bx+c与x轴交于点A、C,与y轴交于点B,它的顶点是D,对称轴是直线x=-2,且OB=OC.
如图,抛物线y=-x2+bx+c与x轴交于点A、C,与y轴交于点B,它的顶点是D,对称轴是直线x=-2,且OB=OC.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
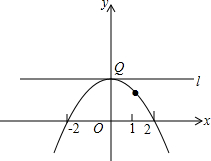 在平面直角坐标系xOy中,已知二次函数y=-$\frac{1}{4}{x}^{2}+mx+n$的图象经过点A(2,0)和点B(1,$\frac{3}{4}$),直线l经过抛物线的顶点且与y轴垂直,垂足为Q.
在平面直角坐标系xOy中,已知二次函数y=-$\frac{1}{4}{x}^{2}+mx+n$的图象经过点A(2,0)和点B(1,$\frac{3}{4}$),直线l经过抛物线的顶点且与y轴垂直,垂足为Q.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
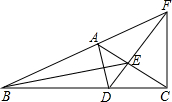 如图,△ABC中,∠BAC=120°,AD为△ABC的内角平分线,CF为△ABC的外角平分线,交BA的延长线于点F,连接DF交AC于E,连接BE,求证:BE平分∠ABC.
如图,△ABC中,∠BAC=120°,AD为△ABC的内角平分线,CF为△ABC的外角平分线,交BA的延长线于点F,连接DF交AC于E,连接BE,求证:BE平分∠ABC.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,A,B两处是我国在南海上的两个观测站,从A处发现它的北偏西30°方向有一艘轮船,同时,从B处发现这艘轮船在它的北偏西60°方向.
如图,A,B两处是我国在南海上的两个观测站,从A处发现它的北偏西30°方向有一艘轮船,同时,从B处发现这艘轮船在它的北偏西60°方向.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com