
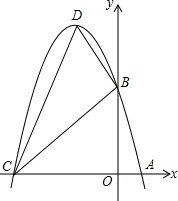
 如图,抛物线y=-x2+bx+c与x轴交于点A、C,与y轴交于点B,它的顶点是D,对称轴是直线x=-2,且OB=OC.
如图,抛物线y=-x2+bx+c与x轴交于点A、C,与y轴交于点B,它的顶点是D,对称轴是直线x=-2,且OB=OC.分析 (1)根据抛物线的对称轴为x=-2,可得出b的值,由OB=OC,可用c表示出C点坐标,代入抛物线解析式即可得得出结论;
(2)由抛物线的解析式可找出B、C、D点的坐标,找出直线BC的解析式,由点到直线的距离结合三角形的面积公式可求出S△BCD,设出P点坐标(m,-m2-4m+5),结合面积相等可得出关于m的一元二次方程,解方程即可得出结论;
(3)构造以B、C、D、E为顶点的平行四边形,就是在△BCD的基础上寻找点E,分别以三角形的三条边为对角线来讨论,即可得出结论.
解答 解:(1)∵抛物线y=-x2+bx+c,对称轴是直线x=-2,
∴$-\frac{b}{2×(-1)}=-2$,得b=-4,
∵抛物线y=-x2+bx+c与x轴交于点A、C,与y轴交于点B,它的顶点是D,且OB=OC,
∴点B的坐标为(0,c),点C的坐标为(-c,0),
∴0=-(-c)2-4×(-c)+c,
解得c=0(舍去)或c=5,
∴抛物线的解析式是y=-x2-4x+5.
(2)∵抛物线的解析式是y=-x2-4x+5=-(x+2)2+9,
∴点D的坐标为(-2,9).
令x=0,y=5,即点B(0,5);
令y=0,-x2-4x+5=0,解得x=-5,或x=1,
即点C(-5,0),点A(1,0).
设点P的坐标为(m,-m2-4m+5),直线BC的解析式为y=kx+5.
∵点C(-5,0)在直线BC上,
∴0=-5k+5,解得:k=1,
即直线BC的解析式为x-y+5=0.
点D(-2,9)到直线BC的距离h=$\frac{|-2-9+5|}{\sqrt{{1}^{2}+(-1)^{2}}}$=3$\sqrt{2}$,BC=$\sqrt{[0-(-5)]^{2}+(5-0)^{2}}$=5$\sqrt{2}$,
△BCD的面积S△BCD=$\frac{1}{2}$BC•h=$\frac{1}{2}$×5$\sqrt{2}$×3$\sqrt{2}$=15.
点P到直线AC的距离d=|-m2-4m+5|,AC=1-(-5)=6,
△ACP的面积S△ACP=$\frac{1}{2}$AC•d=3|-m2-4m+5|=15.
①当点P在x轴上方时,有-m2-4m+5=5,
解得:m=0,或m=-4,
此时点P坐标为(0,5)或(-4,5);
②当点P在x轴下方时,有m2+4m-5=5,
解得:m=-2±$\sqrt{14}$,
此时点P坐标为(-2-$\sqrt{14}$,-5)或(-2+$\sqrt{14}$,-5).
综上可知:点P的坐标为(0,5)、(-4,5)、(-2-$\sqrt{14}$,-5)和(-2+$\sqrt{14}$,-5).
(3)点E在直角坐标平面内,点B、C、D、E是一个平行四边形的四个顶点分三种情况:
①以CD为对角线时,如图1所示.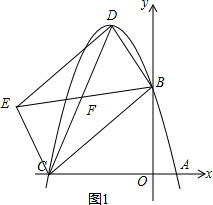
令线段CD的中点为F,由平行四边形的性质可知:
点F为CD的中点,点F还是BE的中点.
∵点C(-5,0),点D(-2,9),
∴xF=$\frac{-5+(-2)}{2}$=-$\frac{7}{2}$,yF=$\frac{0+9}{2}$=$\frac{9}{2}$,
∴点F坐标为(-$\frac{7}{2}$,$\frac{9}{2}$),
∵点B(0,5),
∴xE=2×(-$\frac{7}{2}$)-0=-7,yE=2×$\frac{9}{2}$-5=4,
即此时点E的坐标为(-7,4);
②以BC为对角线,如图2所示.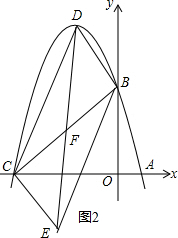
令线段BC的中点为F,由平行四边形的性质可知:
点F为BC的中点,点F还是DE的中点.
∵点B(0,5),点C(-5,0),
∴xF=$\frac{0+(-5)}{2}$=-$\frac{5}{2}$,yF=$\frac{5+0}{2}$=$\frac{5}{2}$,
∴点F的坐标为(-$\frac{5}{2}$,$\frac{5}{2}$),
∵点D(-2,9),
∴xE=2×(-$\frac{5}{2}$)-(-2)=-3,yE=2×$\frac{5}{2}$-9=-4,
即此时点E的坐标为(-3,-4);
③以BD为对角线,如图3所示.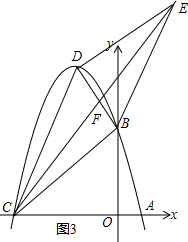
令线段BD的中点为F,由平行四边形的性质可知:
点F为BD的中点,点F还是CE的中点.
∵点B(0,5),点D(-2,9),
∴xF=$\frac{0+(-2)}{2}$=-1,yF$\frac{5+9}{2}$=7,
∴点F的坐标为(-1,7),
∵点C(-5,0),
∴xE=2×(-1)-(-5)=3,yE=2×7-0=14,
即此时点E的坐标为(3,14).
综上可知:满足条件的点E的坐标为:(-7,4)、(-3,-4)和(3,14).
点评 本题考查了解一元二次方程、点到直线的距离、三角形的面积公式、中点坐标公式以及平行四边形的性质,解题的关键是:(1)由OB=OC,以c表示出来C点坐标;(2)由点到直线的距离结合三角形的面积公式找出一元二次方程;(3)在△BCD的基础上构造平行四边形.本题属于中档题,(1)(2)难度不大,在作题的过程中细心计算即可;(3)部分同学感觉无处着手,其实平行四边形是在△BCD的基础上构造的,分别以三角形的三条边为对角线即可解决.


 励耘书业暑假衔接宁波出版社系列答案
励耘书业暑假衔接宁波出版社系列答案科目:初中数学 来源: 题型:选择题
| A. | $\frac{300}{1.2x}$$\frac{300}{x}$=2 | B. | $\frac{300}{x}$-$\frac{300}{1.2x}$=2 | C. | $\frac{300}{1.2x}$=$\frac{300}{x-2}$ | D. | $\frac{300}{x+2}$=$\frac{300}{1.2x}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

| n | an | n | an |
| 1 | 3 | 2 | 6 |
| 3 | 8 | 4 | 11 |
| 5 | 13 | 6 | 16 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
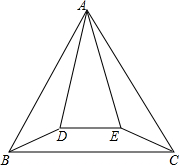 如图,正△ABC与等腰△ADE的顶点A重合,AD=AE,∠DAE=30°,将△ADE绕顶点A旋转,在旋转过程中,当BD=CE时,∠BAD的大小可以是15°或165°.
如图,正△ABC与等腰△ADE的顶点A重合,AD=AE,∠DAE=30°,将△ADE绕顶点A旋转,在旋转过程中,当BD=CE时,∠BAD的大小可以是15°或165°.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
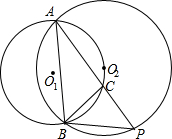 如图,⊙O1与⊙O2都经过A、B两点,且点O2在⊙O1上,点C是弧A O2B上的一动点(点C不与点A、B重合),连接AC并延长AC交O2点P,连接AB,BC,BP,无论点C怎样移动,(1)∠BAP (2)∠APB (3)∠ABC(4)∠ACB(5)∠PBC(6)∠PCB中,大小都不变的角是(2)(4)(5)(6)(填写序号)
如图,⊙O1与⊙O2都经过A、B两点,且点O2在⊙O1上,点C是弧A O2B上的一动点(点C不与点A、B重合),连接AC并延长AC交O2点P,连接AB,BC,BP,无论点C怎样移动,(1)∠BAP (2)∠APB (3)∠ABC(4)∠ACB(5)∠PBC(6)∠PCB中,大小都不变的角是(2)(4)(5)(6)(填写序号)查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com