
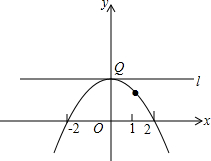 ��ƽ��ֱ������ϵxOy�У���֪���κ���y=-$\frac{1}{4}{x}^{2}+mx+n$��ͼ����A��2��0���͵�B��1��$\frac{3}{4}$����ֱ��l���������ߵĶ�������y�ᴹֱ������ΪQ��
��ƽ��ֱ������ϵxOy�У���֪���κ���y=-$\frac{1}{4}{x}^{2}+mx+n$��ͼ����A��2��0���͵�B��1��$\frac{3}{4}$����ֱ��l���������ߵĶ�������y�ᴹֱ������ΪQ������ ��1����A��B�������ʽ���m��n���ɽ�����⣮
��2����t�Ĵ���ʽ��ʾ�߶�CD��OP��Ȼ�������ֵ���ɣ�
��3���������ľࡢ�뾶���ҳ���һ��֮��Ĺ�ϵ�г����̼��ɽ����
��� �⣺��1���������$\left\{\begin{array}{l}{-1+2m+n=0}\\{-\frac{1}{4}+m+n=\frac{3}{4}}\end{array}\right.$��
���$\left\{\begin{array}{l}{m=0}\\{n=1}\end{array}\right.$��
�ʶ��κ�������ʽΪy=-$\frac{1}{4}$x2+1��
��2����$\frac{CD}{OP}$=$\frac{1}{2}$���������£�
��P����������루1���Ľ���ʽ���ã�$\frac{3}{4}$-2t�T-$\frac{1}{4}$x2+1��x=$\sqrt{8t+1}$��
���P���꣨$\sqrt{8t+1}$��$\frac{3}{4}-2t$����
��OP�е�C�����꣨$\frac{\sqrt{8t+1}}{2}$��$\frac{3}{8}-t$����
��CD=1-��$\frac{3}{8}-t$��=$\frac{5}{8}+t$��OP=$\sqrt{8t+1+��\frac{3}{4}-2t��^{2}}$=2t+$\frac{5}{4}$��
��OP=2CD
��$\frac{CD}{OP}$=$\frac{1}{2}$��
�ڡ�Բ�ĵ�ֱ��l�ľ���d=|$\frac{3}{8}-t$-��1-3t��|=|2t-$\frac{5}{8}$|���뾶r=$\frac{1}{2}$OP=t+$\frac{5}{8}$��EF=$\sqrt{3}$��
�֡ߣ�$\frac{EF}{2}$��2+d2=r2��
��$\frac{3}{4}$+��2t-$\frac{5}{8}$��2=��t+$\frac{5}{8}$��2��
���t=1��$\frac{1}{4}$��
��t=1��$\frac{1}{4}$ʱ����OPΪֱ������C��l���C�Ľ���ΪE��F��EF=$\sqrt{3}$��
���� ���⿼�����ϵ��������κ����Ľ���ʽ��Բ���й�֪ʶ������Ĺؼ�����t�Ĵ���ʽ��ʾ��Ӧ���߶Σ�ѧ�����÷��̵�˼��ȥ˼�����⣬�����п�ѹ���⣮


 ���������ν�ϵ�д�
���������ν�ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
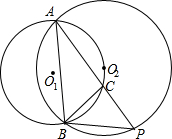 ��ͼ����O1���O2������A��B���㣬�ҵ�O2�ڡ�O1�ϣ���C�ǻ�A O2B�ϵ�һ���㣨��C�����A��B�غϣ�������AC���ӳ�AC��O2��P������AB��BC��BP�����۵�C�����ƶ�����1����BAP ��2����APB ��3����ABC��4����ACB��5����PBC��6����PCB�У���С������Ľ��ǣ�2����4����5����6������д��ţ�
��ͼ����O1���O2������A��B���㣬�ҵ�O2�ڡ�O1�ϣ���C�ǻ�A O2B�ϵ�һ���㣨��C�����A��B�غϣ�������AC���ӳ�AC��O2��P������AB��BC��BP�����۵�C�����ƶ�����1����BAP ��2����APB ��3����ABC��4����ACB��5����PBC��6����PCB�У���С������Ľ��ǣ�2����4����5����6������д��ţ��鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��ͼ�����ı���ABCD�У�AB=AC����ABC=60�㣬��ADC=30�㣬��֤��DB2=DC2+DA2��
��ͼ�����ı���ABCD�У�AB=AC����ABC=60�㣬��ADC=30�㣬��֤��DB2=DC2+DA2���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������

�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com