
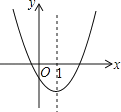
【题目】如图是二次函数 ![]() 的图象的一部分,对称轴是直线
的图象的一部分,对称轴是直线 ![]() . 以下四个判断:①
. 以下四个判断:① ![]() ;②
;② ![]() ;③不等式
;③不等式 ![]() 的解集是
的解集是 ![]() ;④若(
;④若( ![]() ,y1),(5,y2)是抛物线上的两点,则y1<y2。其中正确的是( )
,y1),(5,y2)是抛物线上的两点,则y1<y2。其中正确的是( )
A.①②B.①④C.①③D.②③④
【答案】B
【解析】
根据二次函数的图象与x轴两个交点判断①,当x=2时,求y的值判断②,根据二次函数的图象在y轴上方求得x的取值范围判断③,利用二次函数的增减性判断④.
∵抛物线与x轴有两个交点,
∴b2-4ac>0,即b2>4ac,故①正确;
∵抛物线的对称轴为直线x=0,抛物线与x轴的一个交点横坐标大于2,
∴当x=-2时,4a-2b+c>0,故②错误;
设抛物线与x轴的两交点的横坐标为m,n(m<n)
当x<m或x>n时,ax2+bx+c>0,故③错误;
∵若( ![]() ,y1),(5,y2)是抛物线上的两点,
,y1),(5,y2)是抛物线上的两点,
∵a>0,当x>1时,y随x的增大而增大
当x=-1和x=3时函数值相等,
∴3<5
∴y1<y2 , 故④正确;
正确的有①④.
故答案为:B.


 小学教材全测系列答案
小学教材全测系列答案 小学数学口算题卡脱口而出系列答案
小学数学口算题卡脱口而出系列答案科目:初中数学 来源: 题型:
【题目】在校园文化艺术节中,九年级一班有1名男生和2名女生获得美术奖,另有2名男生和2名女生获得音乐奖.
(1)从获得美术奖和音乐奖的7名学生中选取1名参加颁奖大会,求刚好是男生的概率;
(2)分别从获得美术奖、音乐奖的学生中各选取1名参加颁奖大会,用列表或树状图求刚好是一男生一女生的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
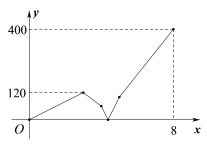
【题目】在一条笔直的公路上顺次有A、B、C三地,甲车从B地出发往A地匀速行驶,到达A地后停止.在甲车出发的同时,乙车也从B地出发往A地匀速行驶,到达A地停留1小时后,调头按原速向C地行驶.若AB两地相距300千米,在两车行驶的过程中,甲、乙两车之间的距离y(千米)与乙车行驶时间x(小时)之间的函数图象如图所示,则在两车出发后经过_____小时相遇.
查看答案和解析>>
科目:初中数学 来源: 题型:
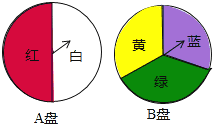
【题目】小颖为班级联欢会设计了一个“配紫色”游戏:下面是两个可以自由转动的转盘,每个转盘被分 成相等的几个扇形.游戏规则是:游戏者同时转动两个转盘,如果转盘 A 转出了红色,转盘 B 转出 了蓝色,那么配成了紫色.
(1)利用树状图或列表的方法计算配成紫色的概率.
(2)小红和小亮参加这个游戏,并约定配成紫色小红赢,两个转盘转出同种颜色,小亮赢.这个约定对双方公平吗?说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图在单位长度为1的正方形网格中,一段圆弧经过网格的交点A、B、C.
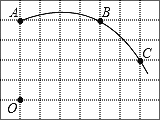
(1)请完成如下操作:
①以点O为坐标原点、竖直和水平方向为轴、网格边长为单位长,建立平面直角坐标系;
②根据图形提供的信息,只借助直尺确定该圆弧所在圆的圆心D,并连接AD、CD.(保留作图痕迹,不写作法)
(2)请在(1)的基础上,完成下列填空与计算:
①写出点的坐标:C 、D ;
②⊙D的半径= ;(结果保留根号)
③求扇形ADC的面积.(结果保留π)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知某二次函数图象的顶点坐标为(1,-4),且经过点C(0,-3)
(1)求这个二次函数的表达式;
(2)求图象与x轴交点A、B两点的坐标(A在点B的左边)及△ABC的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(本小题满分10分)某市政府大力扶持大学生创业.李明在政府的扶持下投资销售一种进价为每件20元的护眼台灯.销售过程中发现,每月销售量y(件)与销售单价x(元)之间的关系可近似的看作一次函数:![]() .
.
(1)设李明每月获得利润为w(元),当销售单价定为多少元时,每月可获得最大利润?
(2)如果李明想要每月获得2000元的利润,那么销售单价应定为多少元?
(3)根据物价部门规定,这种护眼台灯的销售单价不得高于32元,如果李明想要每月获得的利润不低于2000元,那么他每月的成本最少需要多少元?
(成本=进价×销售量)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形ABCD中,AB=3,AD=4,E在AB上,AE=2,HF是CE的垂直平分线,交CD的延长线于点F,连结EF交AD于点G,则![]() 的值是( )
的值是( )
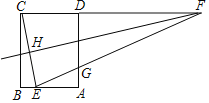
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com