

���� ��1���ٸ��ݵȱ������ε����ʺ�ȫ�������ε��ж�֤����ACD�ա�BCE������ȫ�������ε����ʼ��㼴�ɣ�
�ڸ���ȫ�������ε����ʽ��
��2�����ݵ���ֱ�������ε����ʺ�ȫ�������ε��ж�֤����ACD�ա�BCE������ȫ�������ε����ʼ��㼴�ɣ�
��� �⣺��1���١ߡ�ACB�͡�DCE��Ϊ�ȱ������Σ�
��CA=CB��CD=CE����ACB=��DCE=60�㣬
���ACB-��DCB=��DCE-��DCB������ACD=��BCE��
�ڡ�ACD�͡�BCE�У�
$\left\{\begin{array}{l}{CA=CB}\\{��ACD=��BCE}\\{CD=CE}\end{array}\right.$��
���ACD�ա�BCE��
���CEB=��CDA=120�㣬
���AEB=60�㣬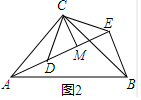
�ʴ�Ϊ��60�㣻
��AD=BE��
֤�����ߡ�ACD�ա�BCE��
��AD=BE��
�ʴ�Ϊ��AD=BE��
��2����AEB=90�㣬AE-BE=2CM��
֤�����ߡ�DCE�ǵ���ֱ�������Σ�CM�����ߣ�
��CM=DM=EM=$\frac{1}{2}$DE��
�ڡ�ACD�͡�BCE�У�
$\left\{\begin{array}{l}{CA=CB}\\{��ACD=��BCE}\\{CD=CE}\end{array}\right.$��
���ACD�ա�BCE��
���CDA=��CEB��
�ߡ�CDA=135�㣬
���AEB=135��-45��=90�㣬
��BE=AD��
��AE-AD=DE=2CM��
��AE-BE=2CM��
���� ���⿼����ǵȱ������ε����ʡ�����ֱ�������ε����ʡ�ȫ�������ε��ж������ʣ����յȱ������ε����ʡ�����ֱ�������ε������ǽ���Ĺؼ���


 ��������һ���þ�ϵ�д�
��������һ���þ�ϵ�д� Сѧ��10����Ӧ����ϵ�д�
Сѧ��10����Ӧ����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
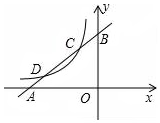 ��ͼ����ֱ֪��y1=x+m��x�ᡢy��ֱ���A��B���㣬��˫����y2=$\frac{k}{x}$�ֱ���C��D���㣬�ҵ�C������Ϊ��-1��2����
��ͼ����ֱ֪��y1=x+m��x�ᡢy��ֱ���A��B���㣬��˫����y2=$\frac{k}{x}$�ֱ���C��D���㣬�ҵ�C������Ϊ��-1��2�����鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
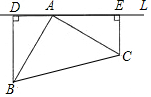 ��ͼ��Rt��ABC�У���BAC=90�㣬AB=AC��BD��ֱ��L��D��CE��ֱ��L��E����BD=5cm��CE=4cm����DE=9cm��
��ͼ��Rt��ABC�У���BAC=90�㣬AB=AC��BD��ֱ��L��D��CE��ֱ��L��E����BD=5cm��CE=4cm����DE=9cm���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��ͼ���ڡ�O���ж���C�Ͷ���Q��λ��ֱ��AB����࣬����C��CP�Ĵ��ߣ���PB���ӳ��߽��ڵ�Q����֪����O�뾶Ϊ$\frac{5}{2}$��tan��ABC=$\frac{3}{4}$�����PCQ��������ֵ��
��ͼ���ڡ�O���ж���C�Ͷ���Q��λ��ֱ��AB����࣬����C��CP�Ĵ��ߣ���PB���ӳ��߽��ڵ�Q����֪����O�뾶Ϊ$\frac{5}{2}$��tan��ABC=$\frac{3}{4}$�����PCQ��������ֵ���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
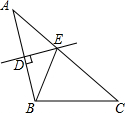 ��ͼ����ABC�У�AC=6��BC=4��AB�Ĵ�ֱƽ����DE��AB�ڵ�D������AC�ڵ�E�����BCE���ܳ�Ϊ10��
��ͼ����ABC�У�AC=6��BC=4��AB�Ĵ�ֱƽ����DE��AB�ڵ�D������AC�ڵ�E�����BCE���ܳ�Ϊ10���鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com