练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    14．64的立方根是（　　）
    A．±8B．±4C．8D．4

    分析 根据开立方的方法，求出$\root{3}{64}$的值，即可判断出64的立方根是多少．

    解答 解：∵$\root{3}{64}$=4，
    ∴64的立方根是4．
    故选：D．

    点评 此题主要考查了立方根的性质和应用，要熟练掌握，解答此题的关键是要明确：一个数的立方根只有一个，正数的立方根是正数，负数的立方根是负数，0的立方根是0．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：解答题

    4．已知：在Rt△ABD中，∠ADB=90°，∠ABD=45°，点F为直线AD上任意一点，过点A作直线AC⊥BF，垂足为点E，直线AC交直线BD于点C，过点F作FG∥BD，交直线AB于点G．
    【问题探究】
    （1）如图1，点F在边AD上，则线段GF、DC、BD之间满足的数量关系是GF+DC=BD；
    【变式探究】
    （2）如图2，若点F在边AD的延长线上，猜想线段FG、DC、BD之间满足的数量关系，并证明你的结论；
    【迁移拓展】
    （3）如图3，在（2）在条件下，在DF=6，GF=10，将一个45°角的顶点与点B重合，并绕点B旋转，这个角的两边分别交线段FG于M、N两点，当FM=2时，求线段NG的长．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

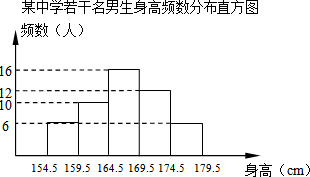    5．为了解某中学300名男生的身高情况，现随机抽取若干名男生进行身高测量，将所得数据整理后，画出频数分布直方图（如图），估计该校男生的身高在169.5cm～174.5cm之间的人数有72人．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    2．计算（$\sqrt{6}$-$\sqrt{2}$）×$\sqrt{2}$=2$\sqrt{3}$-2．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    9．一个不透明的袋中，装有编号为①、②、③、④的四个球，它们除了编号外其余都相同．
    （1）从袋中任意摸出一个球，摸到编号为奇数的球的概率为$\frac{1}{2}$；
    （2）从袋中任意摸出两个球，求摸到的球编号都为奇数的概率．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    19．若一个凸n边形的内角和为1080°，则边数n=8．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

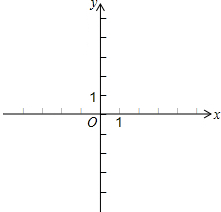    6．已知一次函数y1=kx+b（k≠0）的图象经过（2，0），（4，1）两点，二次函数y2=x2-2ax+4（其中a＞2）．
    （1）求一次函数的表达式及二次函数图象的顶点坐标（用含a的代数式表示）；
    （2）利用函数图象解决下列问题：
    ①若a=$\frac{5}{2}$，求当y1＞0且y2≤0时，自变量x的取值范围；
    ②如果满足y1＞0且y2≤0时的自变量x的取值范围内恰有一个整数，直接写出a的取值范围．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    3．如图，四边形ABCD是⊙O的内接四边形，若∠C=130°，则∠BOD=100°．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

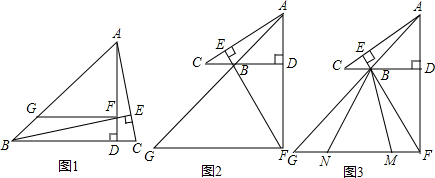
    4．如图，在电线杆上的C处引拉线CE，CF固定电线杆，拉线CE和地面成50°角，在离电线杆底部D点6米的B处安置测角仪，测角仪高AB为1.5米，在A处测得电线杆上C处的仰角为32°，求拉线CE的长（结果精确到0.1米）．（参考数据：sin32°≈0.53，cos32°≈0.85，tan32°≈0.63，sin50°≈0.77，cos50°≈0.64，tan50°≈1.19）．

    查看答案和解析>>

    同步练习册答案