
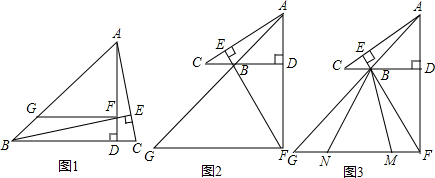
分析 (1)先证明△BDF≌△ADC,得出DF=DC,再证明FG=AF,即可得出结论;
(2)过点B作BH⊥GF于点H,由△ABD 和△AGF都是等腰直角三角形.得出AD=BD,AF=FG,再证明△ADC≌△BDF,得出DC=DF,即可得出结论;
(3)作NP⊥AG于P,由四边形DFHB是矩形,△PGN是等腰直角三角形,得出BH=DF=6,PG=PN,设PG=PN=x,则NG=$\sqrt{2}$x,再证出∠PBN=∠MBH,得出tan∠PBN=tan∠MBH=$\frac{1}{3}$,得BP=3PN=3x,列出方程x+3x=6$\sqrt{2}$,解方程即可得出结果.
解答 解:(1)FG+DC=BD;理由:
∵∠ADB=90°,∠ABD=45°,
∴∠ADC=90°,∠BAD=45°,
∴AD=BD,∠C+∠DBF=90°,∠C+∠DAC=90°,
∴∠DBF=∠DAC,
在△BDF和△ADC中,
$\left\{\begin{array}{l}{∠BDF=∠ADC=90°}\\{BD=AD}\\{∠DBF=∠DAC}\end{array}\right.$,
∴△BDF≌△ADC(ASA),
∴DF=DC,
∵FG∥BD,
∴∠AFG=∠ADB=90°,∠AGF=∠ABD=45°,
∴FG=AF,
∴FG+DC=AF+DF=AD=BD;
故答案为:FG+CD=BD;
(2)FG=DC+BD;理由如下:
过点B作BH⊥GF于点H,如图2所示: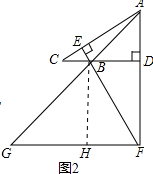 则四边形DFHB是矩形,
则四边形DFHB是矩形,
∵在Rt△ABD中,∠ADB=90°,∠ABD=45°,FG∥BD,
∴△ABD 和△AGF都是等腰直角三角形,
∴AD=BD,AF=FG,
∵AC⊥BF,
∴∠CEB=90°,
∴∠C+∠CBE=90°,
∵∠C+∠DAC=90°,∠CBE=∠DBF,
∴∠DAC=∠DBF,∠ADB=90°,
在△ADC和△BDF中,
$\left\{\begin{array}{l}{∠ADC=∠BDF=90°}\\{AD=BD}\\{∠DAC=∠DBF}\end{array}\right.$,
∴△ADC≌△BDF(ASA),
∴DC=DF,
∴AF=DF+AD=DC+BD,
∴FG=DC+BD;
(3)作NP⊥AG于P,如图3所示: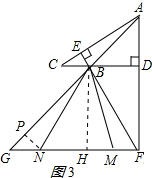 则四边形DFHB是矩形,△PGN是等腰直角三角形,
则四边形DFHB是矩形,△PGN是等腰直角三角形,
∴BH=DF=6,PG=PN,
设PG=PN=x,则NG=$\sqrt{2}$x,
∵∠G=45°,
∴GH=BH=6,BG=6$\sqrt{2}$,∠GBH=45°,
∵∠MBN=45°,
∴∠PBN=∠MBH,
∴tan∠PBN=tan∠MBH=$\frac{2}{6}$=$\frac{1}{3}$,
∴BP=3PN=3x,
∴PG+BP=x+3x=4x=6$\sqrt{2}$,
解得:x=$\frac{3\sqrt{2}}{2}$,
∴NG=$\sqrt{2}$×$\frac{3\sqrt{2}}{2}$=3.
点评 本题考查了全等三角形的判定与性质、等腰直角三角形的判定与性质、勾股定理、锐角三角函数等知识;本题难度较大,综合性强,特别是(2)(3)中,需要通过作辅助线证明等腰直角三角形和运用三角函数才能得出结论.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
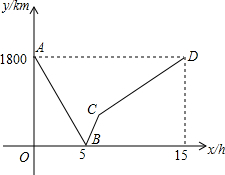 近几年铁路部门为了满足人们的出行需求,做出了许多贡献:线路不断增加,车次越来越多,速度逐渐加快,这给我们的生活带来了许多便利.“五一”期间,小颖决定对重庆到北京这段铁路,火车运行的情况进行调查.某天,他收集到如下信息:现有一列高铁从重庆驶往北京,一列动车从北京驶往重庆(高铁的速度大于动车的速度),两车同时出发并且线路相同,设动车行驶的时间为x(h),两车之间的距离为 y(km),图中的折线表示y与x之间的关系,根据图象进行以下探究:
近几年铁路部门为了满足人们的出行需求,做出了许多贡献:线路不断增加,车次越来越多,速度逐渐加快,这给我们的生活带来了许多便利.“五一”期间,小颖决定对重庆到北京这段铁路,火车运行的情况进行调查.某天,他收集到如下信息:现有一列高铁从重庆驶往北京,一列动车从北京驶往重庆(高铁的速度大于动车的速度),两车同时出发并且线路相同,设动车行驶的时间为x(h),两车之间的距离为 y(km),图中的折线表示y与x之间的关系,根据图象进行以下探究:查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com