
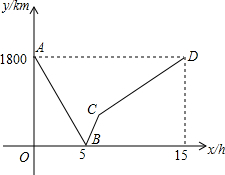
 近几年铁路部门为了满足人们的出行需求,做出了许多贡献:线路不断增加,车次越来越多,速度逐渐加快,这给我们的生活带来了许多便利.“五一”期间,小颖决定对重庆到北京这段铁路,火车运行的情况进行调查.某天,他收集到如下信息:现有一列高铁从重庆驶往北京,一列动车从北京驶往重庆(高铁的速度大于动车的速度),两车同时出发并且线路相同,设动车行驶的时间为x(h),两车之间的距离为 y(km),图中的折线表示y与x之间的关系,根据图象进行以下探究:
近几年铁路部门为了满足人们的出行需求,做出了许多贡献:线路不断增加,车次越来越多,速度逐渐加快,这给我们的生活带来了许多便利.“五一”期间,小颖决定对重庆到北京这段铁路,火车运行的情况进行调查.某天,他收集到如下信息:现有一列高铁从重庆驶往北京,一列动车从北京驶往重庆(高铁的速度大于动车的速度),两车同时出发并且线路相同,设动车行驶的时间为x(h),两车之间的距离为 y(km),图中的折线表示y与x之间的关系,根据图象进行以下探究:分析 (1)根据图形纵坐标直接得出重庆、北京两地之间的距离;
(2)根据图形横坐标直接得出两车同时出发后相遇时间为5小时,动车15小时到达重庆,利用图形得出两车行驶的距离与时间进而得出速度;
(3)根据已知得出C点坐标,进而利用待定系数法求一次函数解析式;
(4)根据在第一列高铁与动车相遇30分钟后,第二列高铁与动车相遇,所以在第一辆高铁开出5.5小时,第二列高铁与动车相遇,设第二辆高铁开出a小时,与动车相遇,则240a+120×5.5=1800,利用时间之差即可解答.
解答 解:(1)由图象可得,重庆、北京两地之间的距离为800km,故答案为:800;
(2)由图形可得:两车同时出发后经5h相遇,动车15小时到达重庆,
∴动车的速度为:1800÷15=120(km/h),
高铁的速度为:(1800÷5)-120=240(km/h).
(3)由题意可得出:B(5,0),
∵高铁的速度为:240km/h,
∴1800÷240=7.5(小时),
C点纵坐标为:120×7.5=900,
∴C(7.5,900),
设线段BC表示的关系为y=kx+b(5≤x≤7.5),
∴$\left\{\begin{array}{l}{5k+b=0}\\{7.5k+b=900}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{k=350}\\{b=-1750}\end{array}\right.$,
∴线段BC表示的关系为y=350x-1750(5≤x≤7.5).
(4)∵在第一列高铁与动车相遇30分钟后,第二列高铁与动车相遇,
∴在第一辆高铁开出5.5小时,第二列高铁与动车相遇,
设第二辆高铁开出a小时,与动车相遇,
则240a+120×5.5=1800,
解得:a=4.75,
5.5-4.75=0.75(小时),
∴第二列高铁比第一列高铁晚出发0.75小时.
点评 本题考查的是用一次函数解决实际问题,此类题是近年中考中的热点问题,关键是根据一次函数的性质和图象结合实际问题判断出每一结论是否正确.


 千里马走向假期期末仿真试卷寒假系列答案
千里马走向假期期末仿真试卷寒假系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
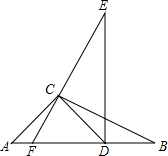 如图,在△ABC中,AC=3$\sqrt{2}$,将△ABC绕点C逆时针转至△DEC的位置,其中点A与点D是对应点,且点D在AB边上,此时BD=3$\sqrt{3}$-3,∠BCD=15°,延长EC交AB于点F.若∠E=30°,则FD=3+$\sqrt{3}$.
如图,在△ABC中,AC=3$\sqrt{2}$,将△ABC绕点C逆时针转至△DEC的位置,其中点A与点D是对应点,且点D在AB边上,此时BD=3$\sqrt{3}$-3,∠BCD=15°,延长EC交AB于点F.若∠E=30°,则FD=3+$\sqrt{3}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 已知△ABC是边长为10cm的等边三角形,一动点D从A出发沿自A向C方向以每秒2cm的速度移动,另一动点E同时从C出发沿自C向B方向以相同速度移动,当点D运动到点C时停止,同时点E也停止运动,连接AE、BD,相交于点F.
已知△ABC是边长为10cm的等边三角形,一动点D从A出发沿自A向C方向以每秒2cm的速度移动,另一动点E同时从C出发沿自C向B方向以相同速度移动,当点D运动到点C时停止,同时点E也停止运动,连接AE、BD,相交于点F.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
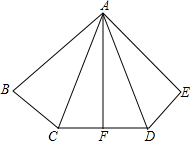 如图,已知AB=AE,∠B=∠E,BC=ED,F是CD的中点.
如图,已知AB=AE,∠B=∠E,BC=ED,F是CD的中点.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
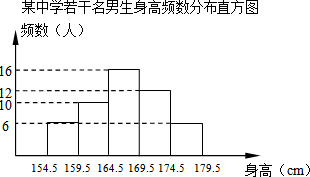 为了解某中学300名男生的身高情况,现随机抽取若干名男生进行身高测量,将所得数据整理后,画出频数分布直方图(如图),估计该校男生的身高在169.5cm~174.5cm之间的人数有72人.
为了解某中学300名男生的身高情况,现随机抽取若干名男生进行身高测量,将所得数据整理后,画出频数分布直方图(如图),估计该校男生的身高在169.5cm~174.5cm之间的人数有72人.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 已知一次函数y1=kx+b(k≠0)的图象经过(2,0),(4,1)两点,二次函数y2=x2-2ax+4(其中a>2).
已知一次函数y1=kx+b(k≠0)的图象经过(2,0),(4,1)两点,二次函数y2=x2-2ax+4(其中a>2).查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com