
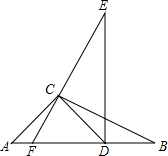
 如图,在△ABC中,AC=3$\sqrt{2}$,将△ABC绕点C逆时针转至△DEC的位置,其中点A与点D是对应点,且点D在AB边上,此时BD=3$\sqrt{3}$-3,∠BCD=15°,延长EC交AB于点F.若∠E=30°,则FD=3+$\sqrt{3}$.
如图,在△ABC中,AC=3$\sqrt{2}$,将△ABC绕点C逆时针转至△DEC的位置,其中点A与点D是对应点,且点D在AB边上,此时BD=3$\sqrt{3}$-3,∠BCD=15°,延长EC交AB于点F.若∠E=30°,则FD=3+$\sqrt{3}$. 分析 由旋转的性质得到CD=AC,DE=AB,∠B=∠E,根据等腰直角三角形的判定得到∠A=∠ADC=45°,∠ACD=90°,通过等量代换得到△DEF是直角三角形,由三角函数即可得到结果.
解答 解:∵△ABC绕点C逆时针转至△DEC,
∴CD=AC,DE=AB,∠B=∠E=30°,
∵∠BCD=15°,
∴∠ADC=45°,
∴∠A=∠ADC=45°,
∴∠ACD=90°,∵AC=3$\sqrt{2}$,
∴AD=6,
∵BD=3$\sqrt{3}$-3,
∴AB=3+3$\sqrt{3}$,
∴DE=3+3$\sqrt{3}$,
∵∠ECD=∠ACB=180°=∠A-∠B=105,
∴∠ECB=∠ECD-∠BCD=90°,
∴∠FCB=90°,
∴∠EFD=60°,
∴∠EDF=90°,
∴DF=tan30°•DE=$\frac{\sqrt{3}}{3}$•(3+3$\sqrt{3}$)=3+$\sqrt{3}$,
故答案为:3+$\sqrt{3}$.
点评 本题考查了图形的变化-旋转,等腰直角三角形的性质,锐角三角函数,掌握旋转的性质是解题的关键.


科目:初中数学 来源: 题型:选择题
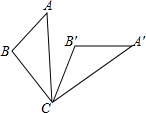 如图,将△ABC绕着点C顺时针旋转60°后得到△A′B′C,若∠A=40°,∠B=110°,则∠BCA′的度数是( )
如图,将△ABC绕着点C顺时针旋转60°后得到△A′B′C,若∠A=40°,∠B=110°,则∠BCA′的度数是( )| A. | 100° | B. | 90° | C. | 70° | D. | 110° |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
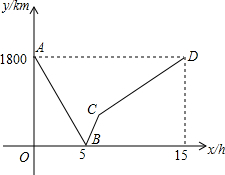 近几年铁路部门为了满足人们的出行需求,做出了许多贡献:线路不断增加,车次越来越多,速度逐渐加快,这给我们的生活带来了许多便利.“五一”期间,小颖决定对重庆到北京这段铁路,火车运行的情况进行调查.某天,他收集到如下信息:现有一列高铁从重庆驶往北京,一列动车从北京驶往重庆(高铁的速度大于动车的速度),两车同时出发并且线路相同,设动车行驶的时间为x(h),两车之间的距离为 y(km),图中的折线表示y与x之间的关系,根据图象进行以下探究:
近几年铁路部门为了满足人们的出行需求,做出了许多贡献:线路不断增加,车次越来越多,速度逐渐加快,这给我们的生活带来了许多便利.“五一”期间,小颖决定对重庆到北京这段铁路,火车运行的情况进行调查.某天,他收集到如下信息:现有一列高铁从重庆驶往北京,一列动车从北京驶往重庆(高铁的速度大于动车的速度),两车同时出发并且线路相同,设动车行驶的时间为x(h),两车之间的距离为 y(km),图中的折线表示y与x之间的关系,根据图象进行以下探究:查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com