在△ABC中.AB=CB.∠ABC=90°.F为AB延长线上一点.点E在BC上.且AE=CF．求证:BE=BF．题目和参考答案——青夏教育精英家教网—

20．在△ABC中，AB=CB，∠ABC=90°，F为AB延长线上一点，点E在BC上，且AE=CF．求证：BE=BF．

分析可根据“HL”判断Rt△ABE≌Rt△CBF，则可得到BE=BF．

解答证明：如图，∵∠ABC=90°，
∴∠CBF=90°
在Rt△ABE和Rt△CBF中，
$\left\{\begin{array}{l}{AB=BC}\\{AE=CF}\end{array}\right.$，
∴Rt△ABE≌Rt△CBF（HL），
∴BE=BF．

点评本题考查了全等三角形的判定与性质：判定三角形全等的方法有“SSS”、“SAS”、“ASA”、“AAS”；全等三角形的对应边相等．也考查了等腰直角三角形的判定与性质．

练习册系列答案

年级	高中课程	年级	初中课程
高一	高一免费课程推荐！	初一	初一免费课程推荐！
高二	高二免费课程推荐！	初二	初二免费课程推荐！
高三	高三免费课程推荐！	初三	初三免费课程推荐！
更多初中、高中辅导课程推荐,点击进入>>

相关习题

科目：初中数学 来源： 题型：解答题

10．

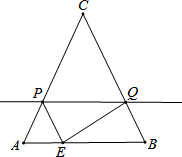已知，如图在△ABC中，AC=BC=10，cos∠CAB=$\frac{3}{5}$与AB重合的直线PQ沿AC方向以1单位/s的速度平移，点E从点A出发沿AB方向以$\frac{6}{5}$单位/s的速度移动，当点E到达B点时，E与PQ同时停止运动．
（1）求AB边上的高及AB的长．
（2）是否存在t使△PEQ为等腰三角形？若存在求出t的值，若不存在请说明理由．
（3）把△PEQ沿直线PQ对折得△PMQ，设△PMQ与△CPQ重叠的面积为S，试求出S关于t的关系式以及其自变量t的取值范围，并求出S的最大值．

查看答案和解析>>

科目：初中数学 来源： 题型：填空题

11．

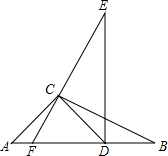如图，在△ABC中，AC=3$\sqrt{2}$，将△ABC绕点C逆时针转至△DEC的位置，其中点A与点D是对应点，且点D在AB边上，此时BD=3$\sqrt{3}$-3，∠BCD=15°，延长EC交AB于点F．若∠E=30°，则FD=3+$\sqrt{3}$．

查看答案和解析>>

科目：初中数学 来源： 题型：解答题

8．

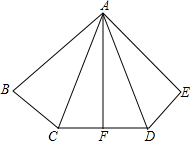如图，已知AB=AE，∠B=∠E，BC=ED，F是CD的中点．
（1）请说明AF⊥CD；
（2）在此图形中，还能得到什么新的结论？（至少写出三个）

查看答案和解析>>

科目：初中数学 来源： 题型：解答题

15．解不等式组：
（1）$\left\{\begin{array}{l}{3x+1＞5-x}\\{2（x+1）-6＜x}\end{array}\right.$．
（2）$\left\{\begin{array}{l}{3x+1＞5（x-1）}\\{\frac{4}{3}x-6≥\frac{6-3x}{3}}\end{array}\right.$．

查看答案和解析>>

科目：初中数学 来源： 题型：解答题

5．

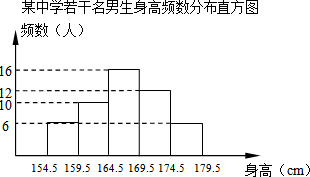为了解某中学300名男生的身高情况，现随机抽取若干名男生进行身高测量，将所得数据整理后，画出频数分布直方图（如图），估计该校男生的身高在169.5cm～174.5cm之间的人数有72人．