
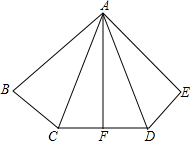
 如图,已知AB=AE,∠B=∠E,BC=ED,F是CD的中点.
如图,已知AB=AE,∠B=∠E,BC=ED,F是CD的中点.科目:初中数学 来源: 题型:解答题
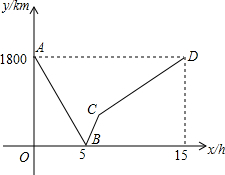 近几年铁路部门为了满足人们的出行需求,做出了许多贡献:线路不断增加,车次越来越多,速度逐渐加快,这给我们的生活带来了许多便利.“五一”期间,小颖决定对重庆到北京这段铁路,火车运行的情况进行调查.某天,他收集到如下信息:现有一列高铁从重庆驶往北京,一列动车从北京驶往重庆(高铁的速度大于动车的速度),两车同时出发并且线路相同,设动车行驶的时间为x(h),两车之间的距离为 y(km),图中的折线表示y与x之间的关系,根据图象进行以下探究:
近几年铁路部门为了满足人们的出行需求,做出了许多贡献:线路不断增加,车次越来越多,速度逐渐加快,这给我们的生活带来了许多便利.“五一”期间,小颖决定对重庆到北京这段铁路,火车运行的情况进行调查.某天,他收集到如下信息:现有一列高铁从重庆驶往北京,一列动车从北京驶往重庆(高铁的速度大于动车的速度),两车同时出发并且线路相同,设动车行驶的时间为x(h),两车之间的距离为 y(km),图中的折线表示y与x之间的关系,根据图象进行以下探究:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
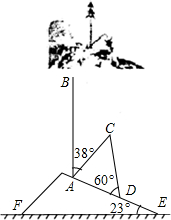 2015年4月25日14时11分尼泊尔发生了8.1级大地震.山坡上有一棵与水平面垂直的大树,大地震过后,大树被刮倾斜后折断倒在山坡上,树的顶部恰好接触到坡面(如图所示).已知山坡的坡角∠AEF=23°,量得树干的倾斜角为∠BAC=38°,大树被折断部分和坡面所成的角∠ADC=60°,AD=4米.
2015年4月25日14时11分尼泊尔发生了8.1级大地震.山坡上有一棵与水平面垂直的大树,大地震过后,大树被刮倾斜后折断倒在山坡上,树的顶部恰好接触到坡面(如图所示).已知山坡的坡角∠AEF=23°,量得树干的倾斜角为∠BAC=38°,大树被折断部分和坡面所成的角∠ADC=60°,AD=4米.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com