
 已知△ABC是边长为10cm的等边三角形,一动点D从A出发沿自A向C方向以每秒2cm的速度移动,另一动点E同时从C出发沿自C向B方向以相同速度移动,当点D运动到点C时停止,同时点E也停止运动,连接AE、BD,相交于点F.
已知△ABC是边长为10cm的等边三角形,一动点D从A出发沿自A向C方向以每秒2cm的速度移动,另一动点E同时从C出发沿自C向B方向以相同速度移动,当点D运动到点C时停止,同时点E也停止运动,连接AE、BD,相交于点F.分析 (1)根据题意得出AD=CE,由等边三角形的性质得出AB=BC=AC,∠BAC=∠ABC=∠C=60°,根据SAS证明△ACE≌△ABD,即可得出AE=BD;
(2)由△ACE≌△ABD,得出∠ABD=∠CAE,即可得出∠AFD=∠BAC=60°.
解答 解:(1)认同AE=BD;理由如下:
根据题意得:AD=CE,
∵△ABC是等边三角形,
∴AB=BC=AC,∠BAC=∠ABC=∠C=60°,
在△ACE和△ABD中,$\left\{\begin{array}{l}{AC=AB}&{\;}\\{∠C=∠BAD}&{\;}\\{CE=AD}&{\;}\end{array}\right.$,
∴△ACE≌△ABD(SAS),
∴AE=BD;
(2)这个夹角为60°;理由如下:
∵△ACE≌△ABD,
∴∠ABD=∠CAE,
∴∠AFD=∠ABD+∠BAF=∠CAE+∠BAF=∠BAC=60°,
即直线BD和AE的夹角为60°.
点评 本题考查了等边三角形的性质、全等三角形的判定与性质;熟练掌握等边三角形的性质,并能进行推理论证是解决问题的关键.


 期末金牌卷系列答案
期末金牌卷系列答案 轻松课堂标准练系列答案
轻松课堂标准练系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
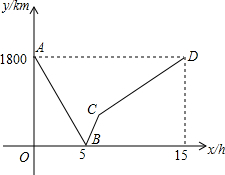 近几年铁路部门为了满足人们的出行需求,做出了许多贡献:线路不断增加,车次越来越多,速度逐渐加快,这给我们的生活带来了许多便利.“五一”期间,小颖决定对重庆到北京这段铁路,火车运行的情况进行调查.某天,他收集到如下信息:现有一列高铁从重庆驶往北京,一列动车从北京驶往重庆(高铁的速度大于动车的速度),两车同时出发并且线路相同,设动车行驶的时间为x(h),两车之间的距离为 y(km),图中的折线表示y与x之间的关系,根据图象进行以下探究:
近几年铁路部门为了满足人们的出行需求,做出了许多贡献:线路不断增加,车次越来越多,速度逐渐加快,这给我们的生活带来了许多便利.“五一”期间,小颖决定对重庆到北京这段铁路,火车运行的情况进行调查.某天,他收集到如下信息:现有一列高铁从重庆驶往北京,一列动车从北京驶往重庆(高铁的速度大于动车的速度),两车同时出发并且线路相同,设动车行驶的时间为x(h),两车之间的距离为 y(km),图中的折线表示y与x之间的关系,根据图象进行以下探究:查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com