
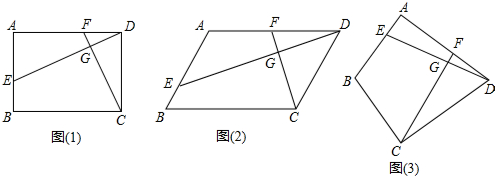
 如图,已知E、F是平行四边形ABCD对角线BD的三等分点,且CG=3,则AD等于
如图,已知E、F是平行四边形ABCD对角线BD的三等分点,且CG=3,则AD等于分析 由E、F是平行四边形ABCD对角线BD的三等分点求出BE与DE比值,再由平行四边形的对边平行且相等得到AD与BC平行且相等,由两直线平行得到两对内错角相等,进而得到三角形BGE与三角形ADE相似,由相似得比例求出BG与AD比值,即为BG与BC比值,得到G为BC中点,即可求出AD的长.
解答 解:∵E、F是平行四边形ABCD对角线BD的三等分点,
∴BE:ED=1:2,AD∥BC,AD=BC,
∴∠DAE=∠EGB,∠ADE=∠EBG,
∴△BGE∽△DAE,
∴BG:AD=BE:ED=1:2,
即BG:BC=1:2,
∴G为BC中点,
则AD=BC=2CG=6.
故答案为:6.
点评 此题考查了相似三角形的判定与性质,以及平行四边形的性质,熟练掌握相似三角形的判定与性质是解本题的关键.


科目:初中数学 来源: 题型:选择题
| A. | 3.283×104米 | B. | 32.83×104米 | C. | 3.283×105米 | D. | 3.283×103米 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
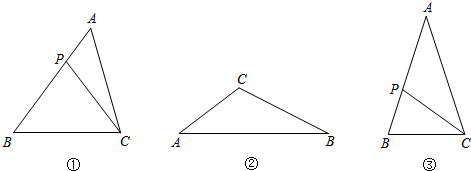
 矩形ADQP∽矩形ABCD,那么就称PQ为矩形ABCD的边AB、CD上的相似线.
矩形ADQP∽矩形ABCD,那么就称PQ为矩形ABCD的边AB、CD上的相似线.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
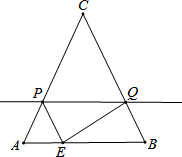 已知,如图在△ABC中,AC=BC=10,cos∠CAB=$\frac{3}{5}$与AB重合的直线PQ沿AC方向以1单位/s的速度平移,点E从点A出发沿AB方向以$\frac{6}{5}$单位/s的速度移动,当点E到达B点时,E与PQ同时停止运动.
已知,如图在△ABC中,AC=BC=10,cos∠CAB=$\frac{3}{5}$与AB重合的直线PQ沿AC方向以1单位/s的速度平移,点E从点A出发沿AB方向以$\frac{6}{5}$单位/s的速度移动,当点E到达B点时,E与PQ同时停止运动.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
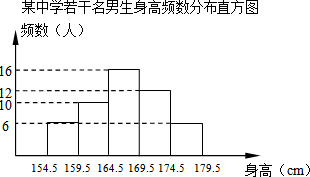 为了解某中学300名男生的身高情况,现随机抽取若干名男生进行身高测量,将所得数据整理后,画出频数分布直方图(如图),估计该校男生的身高在169.5cm~174.5cm之间的人数有72人.
为了解某中学300名男生的身高情况,现随机抽取若干名男生进行身高测量,将所得数据整理后,画出频数分布直方图(如图),估计该校男生的身高在169.5cm~174.5cm之间的人数有72人.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com