
【题目】如图1是一张长方形的纸带,将这张纸带沿EF折叠成图2,再沿BF折叠成图3.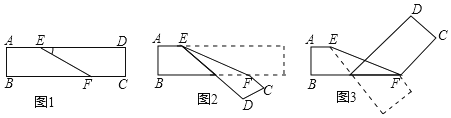
(1)若∠DEF=20°,请你求出图3中∠CFE度数;
(2)若∠DEF=a,请你直接用含a的式子表示图3中∠CFE的度数.
【答案】
(1)解:∵矩形对边AD∥BC,
∴CF∥DE,
∴图1中,∠CFE=180°﹣∠DEF=180°﹣20°=160°,
∵矩形对边AD∥BC,
∴∠BFE=∠DEF=20°,
∴图2中,∠BFC=160°﹣20°=140°,
由翻折的性质得,图3中∠CFE+∠BFE=∠BFC,
∴图3中,∠CFE+20°=140°,
∴图3中,∠CFE=120°
(2)解: 
∵矩形对边AD∥BC,
∴CF∥DE,
∴图1中,∠CFE=180°﹣∠DEF=180°﹣a,
∵矩形对边AD∥BC,
∴∠BFE=∠DEF=a,
∴图2中,∠BFC=180°﹣2a,
由翻折的性质得,图3中∠CFE+∠BFE=∠BFC,
∴图3中,∠CFE+a=180°﹣2a,
∴图3中,∠CFE=180°﹣3a.
【解析】根据矩形的性质可解.
【考点精析】关于本题考查的平行线的性质,需要了解两直线平行,同位角相等;两直线平行,内错角相等;两直线平行,同旁内角互补才能得出正确答案.


科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠A=90°,AB=AC,BC=20,DE是△ABC的中位线,点M是边BC上一点,BM=3,点N是线段MC上的一个动点,连接DN,ME,DN与ME相交于点O.若△OMN是直角三角形,则DO的长是 . 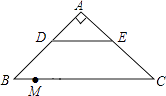
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在Rt△ABC中,∠C=90°,D、E、F分别为AB、BC、AC边上的中点,AC=4cm,BC=6cm,那么四边形CEDF为 , 它的边长分别为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,小华站在河岸上的G点,看见河里有一小船沿垂直于岸边的方向划过来.此时,测得小船C的俯角是∠FDC=30°,若小华的眼睛与地面的距离是1.6米,BG=0.7米,BG平行于AC所在的直线,迎水坡i=4:3,坡长AB=8米,点A、B、C、D、F、G在同一平面内,则此时小船C到岸边的距离CA的长为 米.(结果保留根号)
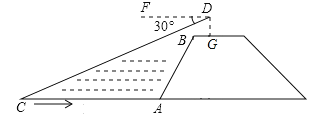
查看答案和解析>>
科目:初中数学 来源: 题型:
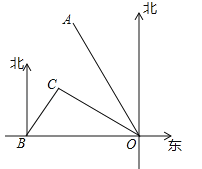
【题目】如图所示,港口B位于港口O正西方向120km处,小岛C位于港口O北偏西60°的方向.一艘游船从港口O出发,沿OA方向(北偏西30°)以vkm/h的速度驶离港口O,同时一艘快艇从港口B出发,沿北偏东30°的方向以60km/h的速度驶向小岛C,在小岛C用1h加装补给物资后,立即按原来的速度给游船送去.
(1)快艇从港口B到小岛C需要多长时间?
(2)若快艇从小岛C到与游船相遇恰好用时1h,求v的值及相遇处与港口O的距离.
查看答案和解析>>
科目:初中数学 来源: 题型:
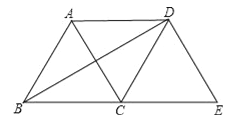
【题目】如图,将等边△ABC绕点C顺时针旋转120°得到△EDC,连接AD,BD.则下列结论:
①AC=AD;②BD⊥AC;③四边形ACED是菱形.
其中正确的个数是( )
A.0 B.1 C.2 D.3
查看答案和解析>>
科目:初中数学 来源: 题型:
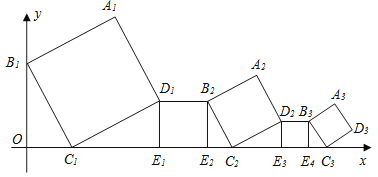
【题目】一组正方形按如图所示的方式放置,其中顶点B1在y轴上,顶点C1、E1、E2、C2、E3、E4、C3…在x轴上,已知正方形A1B1C1D1的边长为1,∠B1C1O=60°,B1C1∥B2C2∥B3C3…则正方形A2016B2016C2016D2016的边长是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com