
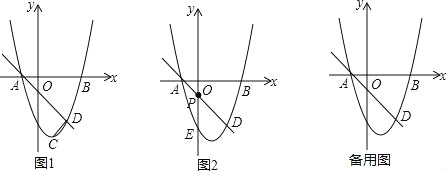
����Ŀ����ͼ1����֪������y=ax2��2ax��3��x�ύ��A��B���㣬�䶥��ΪC������A��ֱ�߽�����������һ��D��2����3������tan��BAD=1��
��1���������ߵĽ���ʽ��
��2������CD����֤��AD��CD��
��3����ͼ2��P���߶�AD�ϵĶ��㣬����P��y���ƽ���߽��������ڵ�E�����߶�PE���ȵ����ֵ��
��4����Q���������ϵĶ��㣬��x�����Ƿ���ڵ�F��ʹ��A��D��F��QΪ������ı�����ƽ���ı��Σ������ڣ�ֱ��д����F�����ꣻ�������ڣ���˵�����ɣ�
���𰸡���1��y=x2��2x��3����2��֤������������3��![]() ����4�����ڣ�����3��0����4+
����4�����ڣ�����3��0����4+![]() ��0����4��
��0����4��![]() ��0����1��0��.
��0����1��0��.
��������
��1������D��DM��x����M�����ݵ�D���������DM��OM���ٸ��ݡ�BAD������ֵ���AM��Ȼ�����AO���Ӷ��õ���A�����꣬�ٴ��������߱���ʽ���a���Ӷ��ý⣻
��2�����������߽���ʽ�������C�����꣬�����ù��ɶ�����ʽ���AC��CD��AD��Ȼ�����ù��ɶ����涨��֤�����ɣ�
��3�����ô���ϵ�������ֱ��AD�Ľ���ʽ���ٱ�ʾ��PE��Ȼ����ݶ��κ�������ֵ������⼴�ɣ�
��4�����F������Ϊ��x��0����Ȼ��֢�AD��ƽ���ı��εı���FQ��x���·�ʱ����ʾ����Q�����꣬Ȼ����������߽���ʽ��⼴�ɣ�FQ��x���Ϸ�ʱ����ʾ����Q�����꣬�ٴ��������߽���ʽ��⣻��AD��ƽ���ı��ζԽ���ʱ������ƽ���ı��ζԱ�ƽ�пɵ�DQ��x�ᣬȻ����ݵ�D�������������Q�����꣬�ٸ���AF=DQ�����F�����꼴�ɣ�
��1����ͼ������D��DM��x����M��
��D��2����3����
��DM=3��OM=2��
��tan��BAD=1��
��AM=DM=3��
��AO=AM��OM=3��2=1��
���A����������1��0����
����A��������������ߵã�a+2a��3=0��
���a=1��
���ԣ�y=x2��2x��3��
��2��֤������y=x2��2x��3=��x��1��2��4��
�ඥ��C��1����4����
�ɹ��ɶ����ã�AD2=32+32=18��
CD2=��2��1��2+����3+4��2=2��
AC2=��1+1��2+42=20��
��AD2+CD2=AC2=20��
���ACD��ֱ�������Σ��ҡ�ADC=90�㣬
��AD��CD��
��3����ֱ��AD�Ľ���ʽΪy=kx+b��k��0����
����A��D���������ã�![]() ��
��
���![]() ��
��
���ԣ�ֱ��AD�Ľ���ʽΪy=��x��1��
���ԣ�PE=����x��1������x2��2x��3��=��x2+x+2=����x��![]() ��2+
��2+![]() ��
��
��P���߶�AD�ϵĶ��㣬
����1��x��2��
�൱x=![]() ʱ���߶�PE���ȵ����ֵ��
ʱ���߶�PE���ȵ����ֵ��![]() ��
��
��4�����F��������x��0����
��AD��ƽ���ı��εı���FQ��x���·�ʱ����Q������Ϊ��x+3����3����
���������ߵã���x+3��2��2��x+3����3=��3��
���x1=��3��x2=��1����ȥ����
���ԣ�F����3��0����
FQ��x���Ϸ�ʱ����Q������Ϊ��x��3��3����
���������ߵã���x��3��2��2��x��3����3=3��
�����ã�x2��8x+9=0��
��ã�x=4��![]() ��
��
���ԣ�F��4+![]() ��0����4��
��0����4��![]() ��0����
��0����
��AD��ƽ���ı��ζԽ���ʱ����A��F����x���ϣ�
��DQ��x�ᣬ
���Q����������3��
��x2��2x��3=��3��
���x1=2��x2=0��
��DQ=2��
��AF=2��
��AO=1��
��OF=2��1=1��
��F��1��0����
����������x���ϴ��ڵ�F����3��0����4+![]() ��0����4��
��0����4��![]() ��0����1��0����ʹ��A��D��F��QΪ������ı�����ƽ���ı��Σ�
��0����1��0����ʹ��A��D��F��QΪ������ı�����ƽ���ı��Σ�


 �����Ծ�ϵ�д�
�����Ծ�ϵ�д� �ο�����������100��ϵ�д�
�ο�����������100��ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
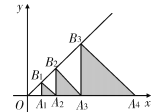
����Ŀ����ͼ����ƽ��ֱ������ϵ�У���A1��A2��A3������x���ϣ���B1��B2��B3������ֱ��y=x�ϣ�OA1=1���ҡ�B1A1A2����B2A2A3����B3A3A4������Bn A n A n+1���ֱ�����A1��A2��A3����An��Ϊֱ�Ƕ���ĵ���ֱ�������Σ����B10A10A11�������________.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��A��B��C��������������Ϸ����Ϸ�����ǣ���һ�δ�����A��������ش���B��C�����е�ijһ�ˣ��Ժ��ÿһ�δ��������ϴεĴ���������ش������������е�ijһ�ˣ�
��1�������δ������ǡ��B���еĸ��ʣ�
��2�������δ������ǡ��A���еĸ���.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
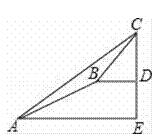
����Ŀ��ij��ѧ��ȤС��ͬѧ���в�������CD�߶ȵ��ۺ�ʵ�������ͼ���ڵ�A�����ֱ���ڵ���Ĵ�������C������Ϊ36����Ȼ������ͬһ�����б��AB����13�����¶�B����Ȼ������ˮƽ��������6���������ŵ�D����б��AB���¶ȣ����±���i=1��2.4�������CD�ĸ߶ȣ����ο����ݣ�sin36���0.59��cos36���0.81��tan36���0.73��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
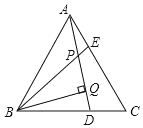
����Ŀ����֪,��ͼ,��ABC�ǵȱ�������,AE=CD,BQ��AD��Q,BE��AD�ڵ�P,����˵�����١�APE=��C,��AQ=BQ,��BP=2PQ,��AE+BD=AB,������ȷ�ĸ�����( )����
A. 4B. 3C. 2D. 1
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����Rt��ABC�У���ACB=90�㣬��A=40�㣬��ABC����ǡ�CBD��ƽ����BE��AC���ӳ����ڵ�E��
��1�����CBE�Ķ�����
��2������D��DF��BE����AC���ӳ����ڵ�F�����F�Ķ�����

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
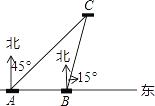
����Ŀ����ͼ��ij�����ҹ�ij�����������������������еĺ��ബA��B������A����������������������20����ľ��룬ijһʱ�������ബͬʱ�����A�Ķ������ı�ƫ��15��������һ�ҹ�����ִ����C�����ʱ��C�봬B�ľ����Ƕ��٣����������С�����һλ��
�ο����ݣ� ![]() ��1.414��
��1.414�� ![]() ��1.732��
��1.732�� ![]() ��2.236��
��2.236��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪һ�κ��� y=kx+b ��ͼ���㣨-1��-5������������������![]() �ڵ㣨2��a������:
�ڵ㣨2��a������:
��1��a ��ֵ��
��2��k��b ��ֵ��
��3������������ͼ���� x ����Χ�ɵ������ε������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
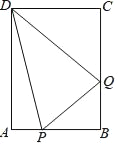
����Ŀ����ͼ������ABCD�У�AB=6cm��BC=8cm����P�ӵ�A�ر�AB��1cm/s���ٶ����B�ƶ���ͬʱ��Q�ӵ�B�ر�BC��2cm/s���ٶ����C�ƶ�����P��Q��������һ���㵽�յ�ʱ������һ����Ҳֹͣ�˶�������DPQ���������PBQ�������19.5cm2ʱ�����P�˶���ʱ�䣮
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com