
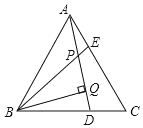
【题目】已知,如图,△ABC是等边三角形,AE=CD,BQ⊥AD于Q,BE交AD于点P,下列说法:①∠APE=∠C,②AQ=BQ,③BP=2PQ,④AE+BD=AB,其中正确的个数有( )个。
A. 4B. 3C. 2D. 1
【答案】B
【解析】
根据等边三角形的性质可得AB=AC,∠BAE=∠C=60°,利用“边角边”证明△ABE和△CAD全等,然后分析判断各选项即可.
证明:∵△ABC是等边三角形,

∴AB=AC,∠BAE=∠C=60°,
在△ABE和△CAD中,
 ,
,
∴△ABE≌△CAD(SAS),
∴∠1=∠2,
∴∠BPQ=∠2+∠3=∠1+∠3=∠BAC=60°,
∴∠APE=∠C=60°,故①正确
∵BQ⊥AD,
∴∠PBQ=90°∠BPQ=90°60°=30°,
∴BP=2PQ.故③正确,
∵AC=BC.AE=DC,
∴BD=CE,
∴AE+BD=AE+EC=AC=AB,故④正确,
无法判断BQ=AQ,故②错误,
故选B.


科目:初中数学 来源: 题型:
【题目】将正面分别标有数字2,3,4的三张形状、大小一样的卡片洗匀后,背面朝上放在桌面上.
(1)随机地抽取一张卡片,求抽到奇数的概率;
(2)随机地抽取一张卡片,将卡片上标有的数字作为十位上的数字(不放回),再随机地抽取一张卡片,将卡片上标有的数字作为个位上的数字,组成的两位数恰好是“23”的概率是多少?
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
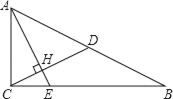
【题目】如图,已知Rt△ABC中,∠ACB=90°,CD是斜边AB上的中线,过点A作AE⊥CD,AE分别与CD、CB相交于点H、E,AH=2CH.
(1)求sinB的值;
(2)如果CD=![]() ,求BE的值.
,求BE的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:直线AB与直线CD交于点O,过点O作OE⊥AB.
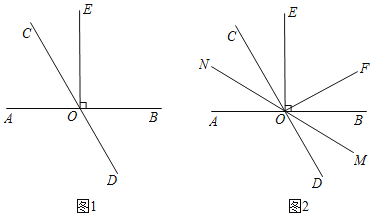
(1)如图1,∠BOC=2∠AOC,求∠COE的度数;
(2)如图2.在(1)的条件下,过点O作OF⊥CD,经过点O画直线MN,满足射线OM平分∠BOD,在不添加任何辅助线的情况下,请直接写出与2∠EOF度数相等的角.
查看答案和解析>>
科目:初中数学 来源: 题型:
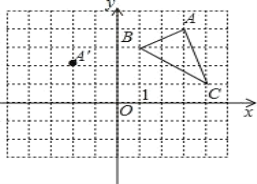
【题目】在平面直角坐标系中,△ABC 的三个顶点的位置如图所示,点 A′的坐标是(-2,2),现将△ABC 平移,使点 A 变换为点 A′,点 B′、C′分别是 B、C 的对应点.
(1) 请画出平移后的△A′B′C′(不写画法),并直接写出点B′、C′的坐标:B′ 、C′ ;
(2) 若△ABC 内部一点 P 的坐标为(![]() ,
,![]() ),则点 P 的对应点 P′的坐标是 ;
),则点 P 的对应点 P′的坐标是 ;
(3) 连接 A′B,CC′,并求四边形 A′BCC′的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
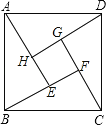
【题目】如图,这个图案是3世纪我国汉代数学家赵爽在注解《周髀算经》时给出的,人们称它为“赵爽弦图”.已知AE=3,BE=2,若向正方形ABCD内随意投掷飞镖(每次均落在正方形ABCD内,且落在正方形ABCD内任何一点的机会均等),则恰好落在正方形EFGH内的概率为_____.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com