
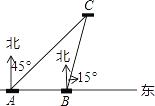
【题目】如图,某日在我国某岛附近海域有两艘自西向东航行的海监船A、B,船在A船的正东方向,且两船保持20海里的距离,某一时刻两海监船同时测得在A的东北方向,的北偏东15°方向有一我国渔政执法船C,求此时船C与船B的距离是多少.(结果保留小数点后一位)
参考数据: ![]() ≈1.414,
≈1.414, ![]() ≈1.732,
≈1.732, ![]() ≈2.236.
≈2.236.
科目:初中数学 来源: 题型:
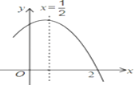
【题目】如图是二次函数y=ax2+bx+c(a≠0)图象的一部分,对称轴为x=![]() ,且经过点(2,0),有下列说法:①abc>0;②a+b=0;③4a+2b+c <0;④若(0,y1),(1,y2)是抛物线上的两点,则y1=y2.上述说法正确的是( )
,且经过点(2,0),有下列说法:①abc>0;②a+b=0;③4a+2b+c <0;④若(0,y1),(1,y2)是抛物线上的两点,则y1=y2.上述说法正确的是( )
A. ①②④ B. ②④ C. ①③④ D. ①②
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】二次函数y=ax2+bx+c,自变量x与函数y的对应值如表:
x | … | ﹣5 | ﹣4 | ﹣3 | ﹣2 | ﹣1 | 0 | … |
y | … | 4 | 0 | ﹣2 | ﹣2 | 0 | 4 | … |
下列说法正确的是( )
A. 抛物线的开口向下
B. 当x>﹣![]() 时,y随x的增大而增大
时,y随x的增大而增大
C. 二次函数的最小值是﹣2
D. 抛物线的对称轴是x=1
查看答案和解析>>
科目:初中数学 来源: 题型:
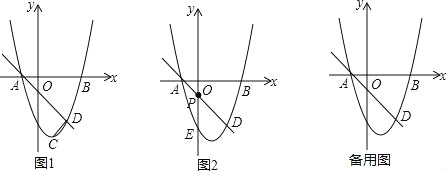
【题目】如图1,已知抛物线y=ax2﹣2ax﹣3与x轴交于A、B两点,其顶点为C,过点A的直线交抛物线于另一点D(2,﹣3),且tan∠BAD=1.
(1)求抛物线的解析式;
(2)连结CD,求证:AD⊥CD;
(3)如图2,P是线段AD上的动点,过点P作y轴的平行线交抛物线于点E,求线段PE长度的最大值;
(4)点Q是抛物线上的动点,在x轴上是否存在点F,使以A,D,F,Q为顶点的四边形是平行四边形?若存在,直接写出点F的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2018年10月,吉州区井冈蜜柚节迎来了四方游客,游客李先生选购了井冈蜜柚和井冈板栗各一箱需要200元.他还准备给4位朋友每人送同样的井冈蜜柚一箱,6位同事每人送同样的井冈板栗一箱,就还需要1040元.
(1)求每箱井冈蜜柚和每箱井冈板栗各需要多少元?
(2)李先生到收银台才得知井冈蜜柚节期间,井冈蜜柚可以享受6折优惠,井冈板栗可以享受8折优惠,此时李先生比预计的付款少付了多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,以AB为直径的⊙O分别与BC,AC相交于点D,E,BD=CD,过点D作⊙O的切线交边AC于点F.
(1)求证:DF⊥AC;
(2)若⊙O的半径为5,∠CDF=30°,求![]() 的长(结果保留π).
的长(结果保留π).

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:等边![]() 中.
中.
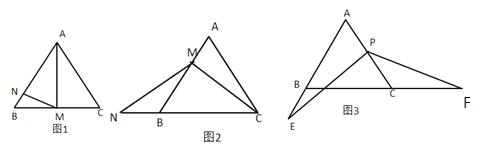
(1)如图1,点![]() 是
是![]() 的中点,点
的中点,点![]() 在
在![]() 边上,满足
边上,满足![]() ,求
,求![]() 的值.
的值.
(2)如图2,点![]() 在
在![]() 边上(
边上(![]() 为非中点,不与
为非中点,不与![]() 、
、![]() 重合),点
重合),点![]() 在
在![]() 的延长线上且
的延长线上且![]() ,求证:
,求证:![]() .
.
(3)如图3,点![]() 为
为![]() 边的中点,点
边的中点,点![]() 在
在![]() 的延长线上,点
的延长线上,点![]() 在
在![]() 的延长线上,满足
的延长线上,满足![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有2个信封,每个信封内各装有四张卡片,其中一个信封内的四张卡片上分别写有1、2、3、4四个数,另一个信封内的四张卡片分别写有5、6、7、8四个数,甲、乙两人商定了一个游戏,规则是:从这两个信封中各随机抽取一张卡片,然后把卡片上的两个数相乘,如果得到的积大于20,则甲获胜,否则乙获胜.
(1)请你通过列表(或画树状图)计算甲获胜的概率
(2)你认为这个游戏公平吗?为什么?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,边长为n的正方形OABC的边OA,OC在坐标轴上,点A1,A2…An﹣1为OA的n等分点,点B1,B2…Bn﹣1为CB的n等分点,连结A1B1,A2B2,…An﹣1Bn﹣1,分别交曲线![]() (x>0)于点C1,C2,…,Cn﹣1.若C15B15=16C15A15,则n的值为_______.(n为正整数)
(x>0)于点C1,C2,…,Cn﹣1.若C15B15=16C15A15,则n的值为_______.(n为正整数)

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com