
【题目】已知:等边![]() 中.
中.
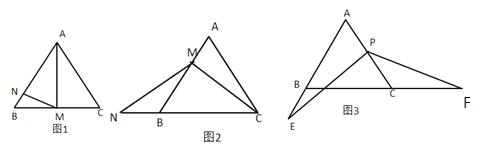
(1)如图1,点![]() 是
是![]() 的中点,点
的中点,点![]() 在
在![]() 边上,满足
边上,满足![]() ,求
,求![]() 的值.
的值.
(2)如图2,点![]() 在
在![]() 边上(
边上(![]() 为非中点,不与
为非中点,不与![]() 、
、![]() 重合),点
重合),点![]() 在
在![]() 的延长线上且
的延长线上且![]() ,求证:
,求证:![]() .
.
(3)如图3,点![]() 为
为![]() 边的中点,点
边的中点,点![]() 在
在![]() 的延长线上,点
的延长线上,点![]() 在
在![]() 的延长线上,满足
的延长线上,满足![]() ,求
,求![]() 的值.
的值.
【答案】(1)3;(2)见解析;(3)![]() .
.
【解析】
(1)先证明![]() ,
,![]() 与
与![]() 均为直角三角形,再根据直角三角形中
均为直角三角形,再根据直角三角形中![]() 所对的直角边等于斜边的一半,证明BM=2BN,AB=2BM,最后转化结论可得出BN与AN之间的数量关系即得;
所对的直角边等于斜边的一半,证明BM=2BN,AB=2BM,最后转化结论可得出BN与AN之间的数量关系即得;
(2)过点M作ME∥BC交AC于E,先证明AM=ME,再证明![]() 与
与![]() 全等,最后转化边即得;
全等,最后转化边即得;
(3)过点P作PM∥BC交AB于M,先证明M是AB的中点,再证明![]() 与
与![]() 全等,最后转化边即得.
全等,最后转化边即得.
(1)∵![]() 为等边三角形,点
为等边三角形,点![]() 是
是![]() 的中点
的中点
∴AM平分∠BAC,![]() ,
,![]()
∴![]() ,
,![]()
∵![]()
∴![]() ,
,![]()
∴![]()
∴![]()
∴在![]() 中,
中,![]()
在![]() 中,
中,![]()
∴![]()
∴![]() 即
即![]() .
.
(2)如下图:
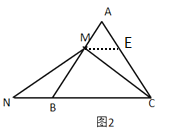
过点M作ME∥BC交AC于E
∴∠CME=∠MCB,∠AEM=∠ACB
∵![]() 是等边三角形
是等边三角形
∴∠A=∠ABC=∠ACB=![]()
∴![]() ,
,![]()
∴![]() ,
,![]()
∴AM=ME
∵![]()
∴∠CME=∠MNB,MN=MC
∴在![]() 与
与![]() 中
中
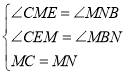
∴![]()
∴![]()
∴![]()
(3)如下图:
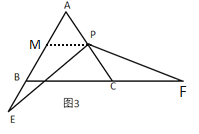
过点P作PM∥BC交AB于M
∴![]()
∵![]() 是等边三角形
是等边三角形
∴∠A=∠ABC=∠ACB=![]() ,
,![]()
∴![]()
∴![]() ,
,![]() ,
,![]()
∴![]() 是等边三角形,
是等边三角形,![]()
∴![]()
∵P点是AC的中点
∴![]()
∴![]()
在![]() 与
与![]() 中
中
∴![]()
∴![]()
∴![]()
∴ .
.


科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC,∠ABC=75°,E为BC延长线上一点,∠ABC与∠ACE的平分线相交于点D.则∠D的度数为( )

A.15°B.17.5°C.20°D.22.5°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,如图,△ABC是等边三角形,AE=CD,BQ⊥AD于Q,BE交AD于点P,下列说法:①∠APE=∠C,②AQ=BQ,③BP=2PQ,④AE+BD=AB,其中正确的个数有( )个。
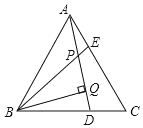
A. 4B. 3C. 2D. 1
查看答案和解析>>
科目:初中数学 来源: 题型:
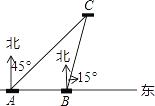
【题目】如图,某日在我国某岛附近海域有两艘自西向东航行的海监船A、B,船在A船的正东方向,且两船保持20海里的距离,某一时刻两海监船同时测得在A的东北方向,的北偏东15°方向有一我国渔政执法船C,求此时船C与船B的距离是多少.(结果保留小数点后一位)
参考数据: ![]() ≈1.414,
≈1.414, ![]() ≈1.732,
≈1.732, ![]() ≈2.236.
≈2.236.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下列一段文字,然后回答下列问题.
已知平面内两点 M(x1,y1)、N(x2,y2),则这两点间的距离可用下列公式计算: MN= ![]() .
.
例如:已知 P(3,1)、Q(1,﹣2),则这两点间的距离 PQ=![]() =
=![]() .
.
特别地,如果两点 M(x1,y1)、N(x2,y2)所在的直线与坐标轴重合或平行于坐标轴或垂直于坐 标轴,那么这两点间的距离公式可简化为 MN=丨 x1﹣x2 丨或丨 y1﹣y2 丨.
(1)已知 A(1,2)、B(﹣2,﹣3),试求 A、B 两点间的距离;
(2)已知 A、B 在平行于 x 轴的同一条直线上,点 A 的横坐标为 5,点 B 的横坐标为﹣1,
试求 A、B 两 点间的距离;
(3)已知△ABC 的顶点坐标分别为 A(0,4)、B(﹣1,2)、C(4,2),你能判定△ABC 的形状 吗?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知一次函数 y=kx+b 的图象经过点(-1,-5),且与正比例函数![]() 于点(2,a),求:
于点(2,a),求:
(1)a 的值;
(2)k,b 的值;
(3)这两个函数图象与 x 轴所围成的三角形的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知像这样由7个全等的正六边形组成的图形叫做“二环蜂窝”,每个正六边形的顶点叫做格点,顶点都在格点上的三角形叫做格点三角形.已知△ABC为该二环蜂窝一个格点三角形,则在该二环蜂窝中,以点A为顶点且与△ABC相似(包括全等但不与△ABC重合)的格点三角形最多能作的个数为( )
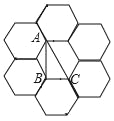
A. 18 B. 23 C. 25 D. 28
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,C为线段AE上一动点(不与点A、E重合),在AE同侧分别作正△ABC和正△CDE,AD与BE交于点O,AD与BC交于点P,BE与CD交于点Q,连接PQ.以下五个结论:①AD=BE;②PQ∥AE;③AP=BQ;④DE=DP;⑤∠AOB=60°.
恒成立的结论有 .(把你认为正确的序号都填上)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在读书月活动中,学校准备购买一批课外读物.为使课外读物满足同学们的需求,学校就“我最喜爱的课外读物”从文学、艺术、科普和其他四个类别进行了抽样调查(每位同学只选一类),如图是根据调查结果绘制的两幅不完整的统计图.

请你根据统计图提供的信息,解答下列问题:
(1)本次调查中,一共调查了 名同学;
(2)条形统计图中,m= ,n= ;
(3)扇形统计图中,艺术类读物所在扇形的圆心角是 度;
(4)学校计划按文学、艺术、科普和其他四个类别购买课外读物 9000 册,请根据样本数据,估计学校购买其他类读物 册比较合理.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com