
【题目】如图,在平面直角坐标系中,矩形ABCO的边OC、OA,分别在x轴、y轴上,点E在边BC上,将该矩形沿AE折叠,点B恰好落在边OC上的F处,若OA=8,CF=4,则点E的坐标是 . 
【答案】(-10,3)
【解析】解:∵矩形ABCO中,
∴CE∥AO.
∴△CEF∽△OFA.
∴![]() =
=![]() .
.
又∵OA=8,CF=4.
∴OF=2CE.
设CE=x,则BE=8-x.
根据折叠的性质,可得EF=8-x.
∴![]() ,
,
∴x=3,
∴OF=6,
∴OC=10,
∴点E的坐标为(-10,3).
故答案为:(-10,3)
根据题意可知△CEF∽△OFA,可根据相似三角形的性质对应边成比例,可求得OF=2CE,设CE=x,则BE=8-x,然后根据折叠的性质,可得EF=8-x,根据勾股定理可得 x 2 + 4 2 = ( 8 x ) 2 ,解得x=3,则OF=6,所以OC=10,由此可得点E的坐标为(-10,3).


科目:初中数学 来源: 题型:
【题目】小明上午8点正从家里出发,到书店买书.右图反映了小明买书过程中(从出发到回家)离家的距离y(米)和离家的时间x(分)的关系.
(1)书店离小明家多远?
(2)若小明离开书店返回家时的平均速度比去书店时的平均速度每分钟快15米,问小明几点到家并求小明离开书店后返家过程中y与x的函数关系式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知点B、C、D在同一条直线上,△ABC和△CDE都是等边三角形.BE交AC于F,AD交CE于H,
①求证:△BCE≌△ACD;
②求证:CF=CH;
③判断△CFH的形状并说明理由。

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,CD∥AB,点O在AB上,OE平分∠BOD,OF⊥OE,∠D=110°.

(1)求∠DOE的度数;
(2)OF平分∠AOD吗?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在矩形ABCD中,AB=12cm,BC=6cm,点P沿AB边从点A开始向点B以2cm/秒的速度移动,点Q沿DA边从点D开始向点A以1cm/秒的速度移动,如果P、Q同时出发,用t(秒)表示运动时间(0≤t≤6),那么当t为何值时,△APQ与△ABD相似?说明理由. 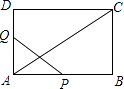
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下列解题过程
已知a、b、c为△ABC为三边,且满足a2c2-b2c2=a4-b4,试判断△ABC的形状
解:∵a2c2-b2c2=a4-b4①
∴c2(a2-b2)=(a2-b2)(a2+b2)②
∴c2=a2+b2③
∴△ABC是直角三角形
回答下列问题:
(1)上述解题过程,从哪一步开始出现错误?请写出该步的序号________.
(2)错误原因为________.
(3)本题正确结论是什么,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场一种商品的进价为每件30元,售价为每件40元.每天可以销售48件,为尽快减少库存,商场决定降价促销.
(1)若该商品连续两次下调相同的百分率后售价降至每件32.4元,求两次下降的百分率;
(2)经调查,若每降价0.5元,每天可多销售4件,那么每天要想获得510元的利润,每件应降价多少元?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校为了解本校的选修课教学,校教务处在七、八年级所有班级中,每班随机抽取了6名学生,并对他们的选修课喜欢程度情况进行了问卷调查,喜欢程度分为:“A﹣非常喜欢”、“B﹣比较喜欢”、“C﹣不太喜欢”、“D﹣很不喜欢”,针对这个题目,问卷时要求每位被调查的学生必须从中选一项且只能选一项.现将统计结果绘制成如下两幅不完整的统计图.

请你根据以上提供的信息,解答下列问题:
(1)补全上面的条形统计图和扇形统计图;
(2)若接核七、八年级共有700名学生,请你估境该年级学生中对远修课“不太喜欢”的有多少人?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com