
 如图,正六边形ABCDEF内接于⊙O,连结AC,EB,CH=6$\sqrt{3}$,则EH的长为( )
如图,正六边形ABCDEF内接于⊙O,连结AC,EB,CH=6$\sqrt{3}$,则EH的长为( )| A. | 12$\sqrt{3}$ | B. | 18 | C. | 6$\sqrt{3}$+6 | D. | 12 |
 第三学期赢在暑假系列答案
第三学期赢在暑假系列答案 学练快车道快乐假期暑假作业新疆人民出版社系列答案
学练快车道快乐假期暑假作业新疆人民出版社系列答案科目:初中数学 来源: 题型:解答题
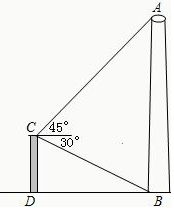 如图,在城市改造时,要拆除建筑物AB,在离它21米远的建筑物CD顶端C测得A的仰角45°,B的俯角30°,在点B的35米处有一文物,问:此文物是否在危险区内?请说明理由.(参考数据:$\sqrt{2}$≈1.414,$\sqrt{3}$≈1.732)
如图,在城市改造时,要拆除建筑物AB,在离它21米远的建筑物CD顶端C测得A的仰角45°,B的俯角30°,在点B的35米处有一文物,问:此文物是否在危险区内?请说明理由.(参考数据:$\sqrt{2}$≈1.414,$\sqrt{3}$≈1.732)查看答案和解析>>
科目:初中数学 来源: 题型:选择题
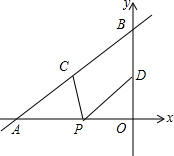 如图,直线y=$\frac{2}{3}$x+4与x轴,y轴分别交于点A和点B,点C,D分别为线段AB,OB的中点,点P为OA上一动点,则PC+PD的最小值为( )
如图,直线y=$\frac{2}{3}$x+4与x轴,y轴分别交于点A和点B,点C,D分别为线段AB,OB的中点,点P为OA上一动点,则PC+PD的最小值为( )| A. | 2+$\sqrt{13}$ | B. | 5 | C. | 2$\sqrt{13}$ | D. | 6 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,已知线段AB=a,延长BA至点C,使AC=$\frac{1}{2}$AB.点D为线段BC的中点.
如图,已知线段AB=a,延长BA至点C,使AC=$\frac{1}{2}$AB.点D为线段BC的中点.查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com