
【题目】如图,菱形ABCD的边长为2,∠A=60°,点P和点Q分别从点B和点C出发,沿射线BC向右运动并且始终保持BP=CQ,过点Q作QH⊥BD,垂足为H,连接PH,设点P运动的距离为x(0<x≤2),△BPH的面积为s,则能反映s与x之间的函数关系的图象大致为 ( )
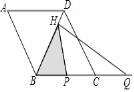
A.  B.
B. 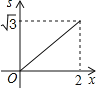 C.
C. 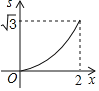 D.
D. 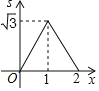
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】今年是中华人民共和国建国70周年,襄阳市某学校开展了“我和我的祖国”主题学习竞赛活动.学校3000名学生全部参加了竞赛,结果所有学生成绩都不低于60分(满分100分).为了了解成绩分布情况,学校随机抽取了部分学生的成绩进行统计,得到如下不完整的统计表.根据表中所给信息,解答下列问题:
成绩 | 频数 | 频率 |
| 15 | 0.30 |
|
| 0.40 |
| 10 |
|
| 5 | 0.10 |
(1)表中![]() ,
,![]() ;
;
(2)这组数据的中位数落在 范围内;
(3)判断:这组数据的众数一定落在![]() 范围内,这个说法 (填“正确”或“错误”);
范围内,这个说法 (填“正确”或“错误”);
(4)这组数据用扇形统计图表示,成绩在![]() 范围内的扇形圆心角的大小为 ;
范围内的扇形圆心角的大小为 ;
(5)若成绩不小于80分为优秀,则全校大约有 名学生获得优秀成绩.
查看答案和解析>>
科目:初中数学 来源: 题型:
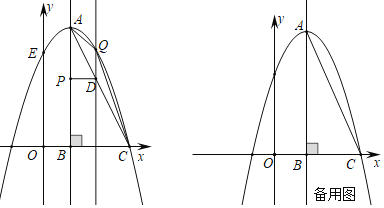
【题目】如图,在平面直角坐标系中,![]() 的边
的边![]() 在
在![]() 轴上,
轴上,![]() ,以
,以![]() 为顶点的抛物线
为顶点的抛物线![]() 经过点
经过点![]() ,交y轴于点
,交y轴于点![]() ,动点
,动点![]() 在对称轴上.
在对称轴上.
(1)求抛物线解析式;
(2)若点![]() 从
从![]() 点出发,沿
点出发,沿![]() 方向以1个单位/秒的速度匀速运动到点
方向以1个单位/秒的速度匀速运动到点![]() 停止,设运动时间为
停止,设运动时间为![]() 秒,过点
秒,过点![]() 作
作![]() 交
交![]() 于点
于点![]() ,过点
,过点![]() 平行于
平行于![]() 轴的直线
轴的直线![]() 交抛物线于点
交抛物线于点![]() ,连接
,连接![]() ,当
,当![]() 为何值时,
为何值时,![]() 的面积最大?最大值是多少?
的面积最大?最大值是多少?
(3)若点![]() 是平面内的任意一点,在
是平面内的任意一点,在![]() 轴上方是否存在点
轴上方是否存在点![]() ,使得以点
,使得以点![]() 为顶点的四边形是菱形,若存在,请直接写出符合条件的
为顶点的四边形是菱形,若存在,请直接写出符合条件的![]() 点坐标;若不存在,请说明理由.
点坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某公司销售部有营业员15人,该公司为了调动营业员的积极性,决定实行目标管理,根据目标完成的情况对营业员进行适当的奖励,为了确定一个适当的月销售目标,公司有关部门统计了这15人某月的销售量,如下表所示:
月销售量/件数 | 1770 | 480 | 220 | 180 | 120 | 90 |
人数 | 1 | 1 | 3 | 3 | 3 | 4 |
(1)直接写出这15名营业员该月销售量数据的平均数、中位数、众数;
(2)如果想让一半左右的营业员都能达到月销售目标,你认为(1)中的平均数、中位数、众数中,哪个最适合作为月销售目标?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】解不等式组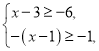
![]() 请结合题意填空,完成本题的解答.
请结合题意填空,完成本题的解答.
(Ⅰ)解不等式①,得_______________;
(Ⅱ)解不等式②,得_______________;
(Ⅲ)把不等式①和②的解集在数轴上表示出来;
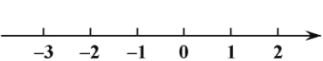
(Ⅳ)原不等式组的解集为____________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示的抛物线是二次函数y=ax2+bx+c(a≠0)的图象,则下列结论:①abc>0;②2a+b=0;③抛物线与x轴的另一个交点为(4,0);④c+a>b;⑤3a+c<0.其中正确的结论有______

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2018年高一新生开始,某省全面启动高考综合改革,实行“3+1+2”的高考选考方案.“3”是指语文、数学、外语三科必考;“1”是指从物理、历史两科中任选一科参加选考,“2”是指从政治、化学、地理、生物四科中任选两科参加选考
(1)“1+2”的选考方案共有多少种?请直接写出所有可能的选法;(选法与顺序无关,例如:“物、政、化”与“物、化、政”属于同一种选法)
(2)高一学生小明和小杰将参加新高考,他们酷爱历史和生物,两人约定必选历史和生物.他们还需要从政治、化学、地理三科中选一科参考,若这三科被选中的机会均等,请用列表或画树状图的方法,求出他们恰好都选中政治的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
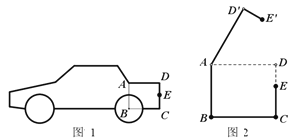
【题目】如图1是某小型汽车的侧面示意图,其中矩形ABCD表示该车的后备箱,在打开后备箱的过程中,箱盖ADE可以绕点A逆时针方向旋转,当旋转角为60°时,箱盖ADE落在AD'E'的位置(如图2所示).已知AD=90厘米,DE=30厘米,EC=40厘米.
(1)求点D'到BC的距离;
(2)求E、E'两点的距离.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com