
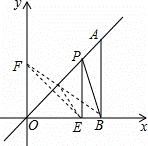
如图,在平面直角坐标系中,A点为直线y=x上一点,过A点作AB⊥x轴于B点,若OB=4,E是OB边上的一点,且OE=3,点P为线段AO上的动点,则△BEP周长的最小值为( )
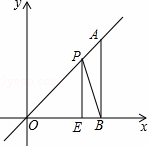
A. 4+2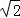 B. 4+
B. 4+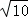 C. 6 D. 4
C. 6 D. 4
C
考点: 轴对称-最短路线问题;一次函数图象上点的坐标特征.
分析: 在y轴的正半轴上截取OF=OE=3,连接EF,证得F是E关于直线y=x的对称点,连接BF交OA于P,此时△BEP周长最小,最小值为BF+EB,根据勾股定理求得BF,因为BE=1,所以△BEP周长最小值为BF+EB=5+1=6.
解答: 解:在y轴的正半轴上截取OF=OE=3,连接EF,
∵A点为直线y=x上一点,
∴OA垂直平分EF,
∴E、F是直线y=x的对称点,
连接BF交OA于P,根据两点之间线段最短可知此时△BEP周长最小,最小值为BF+EB;
∵OF=3,OB=4,
∴BF=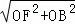 =5,
=5,
∵EB=4﹣3=1,
△BEP周长最小值为BF+EB=5+1=6.
故选C.
点评: 本题考查了轴对称的判定和性质,轴对称﹣最短路线问题,勾股定理的应用等,作出P点是解题的关键.


科目:初中数学 来源: 题型:
如图,在菱形ABCD中,AB=BD.点E、F分别在BC、CD上,且BE=CF.连接BF与DE相交于点G,连接AG与BD相交于点H.下列结论:①△BED≌△CFB;②若DF=2CF,则DG=4GE;③S四边形ABGD=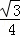 AG2.其中正确的结论( )
AG2.其中正确的结论( )
A.只有②③ B.只有①③ C.只有①② D.①②③
查看答案和解析>>
科目:初中数学 来源: 题型:
如图,边长为(m+3)的正方形纸片,剪出一个边长为m的正方形之后,剩余部分可剪拼成一个矩形(不重叠无缝隙),若拼成的矩形一边长为3,则另一边长是( )
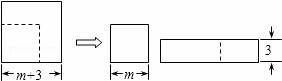
A. m+3 B. m+6 C. 2m+3 D. 2m+6
查看答案和解析>>
科目:初中数学 来源: 题型:
如图,正三角形ABC(图1)和正五边形DEFGH(图2)的边长相同.点O为△ABC的中心,用5个相同的△BOC拼入正五边形DEFGH中,得到图3,则图3中的五角星的五个锐角均为( )
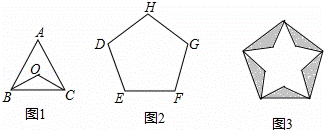
A. 36° B. 42° C. 45° D. 48°
查看答案和解析>>
科目:初中数学 来源: 题型:
如图,某城市中心的两条公路OM和ON,其中OM为东西走向,ON为南北走向,A、B是两条公路所围区域内的两个标志性建筑.已知A、B关于∠MON的平分线OQ对称.OA=1000米,测得建筑物A在公路交叉口O的北偏东53.5°方向上.
求:建筑物B到公路ON的距离.
(参考数据:sin53.5°=0.8,cos53.5°=0.6,tan53.5°≈1.35)
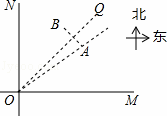
查看答案和解析>>
科目:初中数学 来源: 题型:
已知:如图,在△ABC中,AB=AC,AD⊥BC,垂足为点D,AN是△ABC外角∠CAM的平分线,CE⊥AN,垂足为点E,连接DE交AC于点F.
(1)求证:四边形ADCE为矩形;
(2)当△ABC满足什么条件时,四边形ADCE是一个正方形?并给出证明.
(3)在(2)的条件下,若AB=AC=2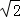 ,求正方形ADCE周长.
,求正方形ADCE周长.
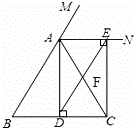
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com