
已知:如图,在△ABC中,AB=AC,AD⊥BC,垂足为点D,AN是△ABC外角∠CAM的平分线,CE⊥AN,垂足为点E,连接DE交AC于点F.
(1)求证:四边形ADCE为矩形;
(2)当△ABC满足什么条件时,四边形ADCE是一个正方形?并给出证明.
(3)在(2)的条件下,若AB=AC=2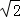 ,求正方形ADCE周长.
,求正方形ADCE周长.
考点: 正方形的判定与性质;矩形的判定.
分析: (1)根据等腰三角形的性质,可得∠CAD= ∠BAC,根据等式的性质,可得∠CAD+∠CAE=
∠BAC,根据等式的性质,可得∠CAD+∠CAE= (∠BAC+∠CAM)=90°,根据垂线的定义,可得∠ADC=∠CEA,根据矩形的判定,可得答案;
(∠BAC+∠CAM)=90°,根据垂线的定义,可得∠ADC=∠CEA,根据矩形的判定,可得答案;
(2)根据等腰直角三角形的性质,可得AD与CD的关系,根据正方形的判定,可得答案;
(3)根据勾股定理,可得AD的长,根据正方形周长公式,可得答案.
解答: (1)证明:∵AB=AC,AD⊥BC,垂足为点D,
∴∠CAD= ∠BAC.
∠BAC.
∵AN是△ABC外角∠CAM的平分线,
∴∠CAE= ∠CAM.
∠CAM.
∵∠BAC与∠CAM是邻补角,
∴∠BAC+∠CAM=180°,
∴∠CAD+∠CAE= (∠BAC+∠CAM)=90°.
(∠BAC+∠CAM)=90°.
∵AD⊥BC,CE⊥AN,
∴∠ADC=∠CEA=90°,
∴四边形ADCE为矩形;
(2)∠BAC=90°且AB=AC时,四边形ADCE是一个正方形,
证明:∵∠BAC=90°且AB=AC,AD⊥BC,
∴∠CAD= ∠BAC=45,∠ADC=90°,
∠BAC=45,∠ADC=90°,
∴∠ACD=∠CAD=45°,
∴AD=CD.
∵四边形ADCE为矩形,
∴四边形ADCE为正方形;
(3)解:由勾股定理,得
 =AB,AD=CD,
=AB,AD=CD,
即 AD=2
AD=2 ,
,
AD=2,
正方形ADCE周长4AD=4×2=8.
点评: 本题考查了的正方形的判定与性质,(1)利用了等腰三角形的性质,矩形的判定;(2)利用了正方形的判定;(3)利用了勾股定理,正方形的周长.


科目:初中数学 来源: 题型:
随着农业科技的不断发展,农田灌溉也开始采用喷灌的形式(如图甲).在田间安装一个离开地面一定高度且垂直于地面的喷头,喷头可旋转360,喷出的水流呈抛物线形状.如图乙,用OA表示垂直于地面MN的喷头,OA=1米,水流在与OA的距离10米时达到最高点,这时最高点离地面5米.如果不计其它因素,当喷头环绕一周后,能喷灌的最大直径是多少米(结果精确到0.1,参考数据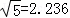 )?
)?
查看答案和解析>>
科目:初中数学 来源: 题型:
如图,在平面直角坐标系中,A点为直线y=x上一点,过A点作AB⊥x轴于B点,若OB=4,E是OB边上的一点,且OE=3,点P为线段AO上的动点,则△BEP周长的最小值为( )
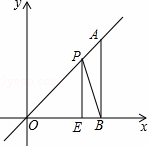
A. 4+2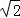 B. 4+
B. 4+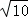 C. 6 D. 4
C. 6 D. 4
查看答案和解析>>
科目:初中数学 来源: 题型:
根据下面表格中的对应值:
x 3.24 3.25 3.26
ax2+bx+c ﹣0.02 0.01 0.03
判断关于x的方程ax2+bx+c=0(a≠0)的一个解x的范围是( )
A. x<3.24 B. 3.24<x<3.25 C. 3.25<x<3.26 D. x>3.26
查看答案和解析>>
科目:初中数学 来源: 题型:
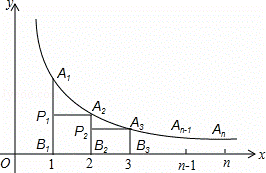
如图,在反比例函数y=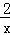 (x>0)的图象上有点A1,A2,A3,…,An﹣1,An,这些点的横坐标分别是1,2,3,…,n﹣1,n时,点A2的坐标是 ;过点A1作x轴的垂线,垂足为B1,再过点A2作A2P1⊥A1B1于点P1,以点P1、A1、A2为顶点的△P1A1A2的面积记为S1,按照以上方法继续作图,可以得到△P2A2A3,…,△Pn﹣1An﹣1An,其面积分别记为S2,…,Sn﹣1,则S1+S2+…+Sn= .
(x>0)的图象上有点A1,A2,A3,…,An﹣1,An,这些点的横坐标分别是1,2,3,…,n﹣1,n时,点A2的坐标是 ;过点A1作x轴的垂线,垂足为B1,再过点A2作A2P1⊥A1B1于点P1,以点P1、A1、A2为顶点的△P1A1A2的面积记为S1,按照以上方法继续作图,可以得到△P2A2A3,…,△Pn﹣1An﹣1An,其面积分别记为S2,…,Sn﹣1,则S1+S2+…+Sn= .
查看答案和解析>>
科目:初中数学 来源: 题型:
如图,已知抛物线y=﹣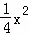 +bx+4与x轴相交于A、B两点,与y轴相交于点C,若已知B点的坐标为B(8,0).
+bx+4与x轴相交于A、B两点,与y轴相交于点C,若已知B点的坐标为B(8,0).
(1)求抛物线的解析式及其对称轴方程.
(2)连接AC、BC,试判断△AOC与△COB是否相似?并说明理由.
(3)在抛物线上BC之间是否存在一点D,使得△DBC的面积最大?若存在请求出点D的坐标和△DBC的面积;若不存在,请说明理由.
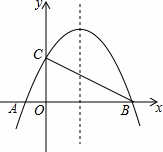
查看答案和解析>>
科目:初中数学 来源: 题型:
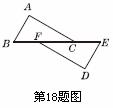
如图,在△ABC和△DEF中,点B、F、C、E在同一直线上,BF=CE, AC∥DF,请添加一个条件,使△ABC≌△DEF,这个添加的条件可以是 .(只需写一个,不添加辅助线)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com