
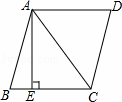
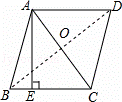
如图,在菱形ABCD中,AB=5,对角线AC=6.若过点A作AE⊥BC,垂足为E,则AE的长为( )
A. 4 B. 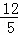 C.
C. 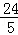 D. 5
D. 5
C考点: 菱形的性质.
专题: 几何图形问题.
分析: 连接BD,根据菱形的性质可得AC⊥BD,AO=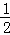 AC,然后根据勾股定理计算出BO长,再算出菱形的面积,然后再根据面积公式BC•AE=
AC,然后根据勾股定理计算出BO长,再算出菱形的面积,然后再根据面积公式BC•AE=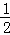 AC•BD可得答案.
AC•BD可得答案.
解答: 解:连接BD,交AC于O点,
∵四边形ABCD是菱形,
∴AB=BC=CD=AD=5,
∴AC⊥BD,AO=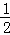 AC,BD=2BO,
AC,BD=2BO,
∴∠AOB=90°,
∵AC=6,
∴AO=3,
∴B0= =4,
=4,
∴DB=8,
∴菱形ABCD的面积是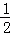 ×AC•DB=
×AC•DB=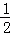 ×6×8=24,
×6×8=24,
∴BC•AE=24,
AE=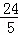 ,
,
故选:C.
点评: 此题主要考查了菱形的性质,以及菱形的性质面积,关键是掌握菱形的对角线互相垂直且平分.


 计算高手系列答案
计算高手系列答案科目:初中数学 来源: 题型:
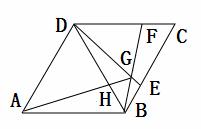
如图,在菱形ABCD中,AB=BD.点E、F分别在BC、CD上,且BE=CF.连接BF与DE相交于点G,连接AG与BD相交于点H.下列结论:①△BED≌△CFB;②若DF=2CF,则DG=4GE;③S四边形ABGD=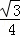 AG2.其中正确的结论( )
AG2.其中正确的结论( )
A.只有②③ B.只有①③ C.只有①② D.①②③
查看答案和解析>>
科目:初中数学 来源: 题型:
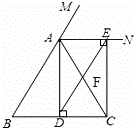
已知:如图,在△ABC中,AB=AC,AD⊥BC,垂足为点D,AN是△ABC外角∠CAM的平分线,CE⊥AN,垂足为点E,连接DE交AC于点F.
(1)求证:四边形ADCE为矩形;
(2)当△ABC满足什么条件时,四边形ADCE是一个正方形?并给出证明.
(3)在(2)的条件下,若AB=AC=2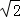 ,求正方形ADCE周长.
,求正方形ADCE周长.
查看答案和解析>>
科目:初中数学 来源: 题型:
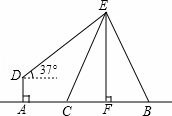
.如图,在电线杆上的E处引拉线EC和EB固定电线杆,在离电线杆6米的A处安置测角仪(点A,C,F在一直线上),在D处测得电线杆上E处的仰角为37°,已知测角仪的高AD为1.5米,AC为3米,求拉线EC的长.(精确到0.1米)
查看答案和解析>>
科目:初中数学 来源: 题型:
下列去括号正确的是( )
A. 3x﹣(2x﹣1)=3x﹣2x﹣1 B. ﹣4(x+1)+5=﹣4x+4+5
C. 2x+7(x﹣1)=2x+7x﹣1 D. 2﹣[3x﹣5(x+1)]=2﹣3x+5x+5
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com