
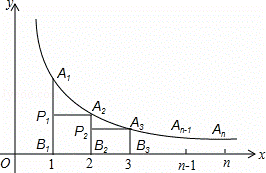
如图,在反比例函数y=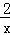 (x>0)的图象上有点A1,A2,A3,…,An﹣1,An,这些点的横坐标分别是1,2,3,…,n﹣1,n时,点A2的坐标是 ;过点A1作x轴的垂线,垂足为B1,再过点A2作A2P1⊥A1B1于点P1,以点P1、A1、A2为顶点的△P1A1A2的面积记为S1,按照以上方法继续作图,可以得到△P2A2A3,…,△Pn﹣1An﹣1An,其面积分别记为S2,…,Sn﹣1,则S1+S2+…+Sn= .
(x>0)的图象上有点A1,A2,A3,…,An﹣1,An,这些点的横坐标分别是1,2,3,…,n﹣1,n时,点A2的坐标是 ;过点A1作x轴的垂线,垂足为B1,再过点A2作A2P1⊥A1B1于点P1,以点P1、A1、A2为顶点的△P1A1A2的面积记为S1,按照以上方法继续作图,可以得到△P2A2A3,…,△Pn﹣1An﹣1An,其面积分别记为S2,…,Sn﹣1,则S1+S2+…+Sn= .
(2,1) 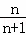
考点: 反比例函数系数k的几何意义;反比例函数图象上点的坐标特征.
专题: 规律型.
分析: 求出x=2所对应的函数值即可确定A2的坐标;根据反比例函数图象上点的坐标特征和三角形面积公式得到S1=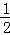 ×1×(2﹣1),S2=
×1×(2﹣1),S2=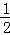 ×1×(1﹣
×1×(1﹣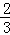 ),S3=
),S3=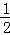 ×1×(
×1×(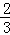 ﹣
﹣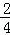 ),…,Sn=
),…,Sn= ×1×(
×1×(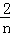 ﹣
﹣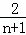 ),然后把它们相加后合并即可.
),然后把它们相加后合并即可.
解答: 解:把x=2代入y= 得y=1,
得y=1,
∴点A2的坐标为(2,1);
∵S1= ×1×(2﹣1),S2=
×1×(2﹣1),S2= ×1×(1﹣
×1×(1﹣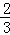 ),S3=
),S3= ×1×(
×1×(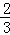 ﹣
﹣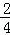 ),…,Sn=
),…,Sn= ×1×(
×1×(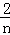 ﹣
﹣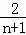 ),
),
∴S1+S2+…+Sn= (2﹣1+1﹣
(2﹣1+1﹣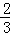 +
+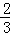 ﹣
﹣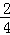 +…+
+…+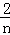 ﹣
﹣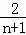 )=
)= (2﹣
(2﹣ )=
)=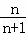 .
.
故答案为(2,1); 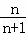 .
.
点评: 本题考查了反比例函数的比例系数k的几何意义:在反比例函数y= 图象中任取一点,过这一个点向x轴和y轴分别作垂线,与坐标轴围成的矩形的面积是定值|k|.
图象中任取一点,过这一个点向x轴和y轴分别作垂线,与坐标轴围成的矩形的面积是定值|k|.


 夺冠金卷全能练考系列答案
夺冠金卷全能练考系列答案科目:初中数学 来源: 题型:
如图,正三角形ABC(图1)和正五边形DEFGH(图2)的边长相同.点O为△ABC的中心,用5个相同的△BOC拼入正五边形DEFGH中,得到图3,则图3中的五角星的五个锐角均为( )
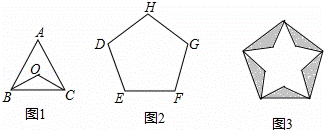
A. 36° B. 42° C. 45° D. 48°
查看答案和解析>>
科目:初中数学 来源: 题型:
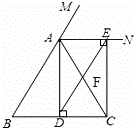
已知:如图,在△ABC中,AB=AC,AD⊥BC,垂足为点D,AN是△ABC外角∠CAM的平分线,CE⊥AN,垂足为点E,连接DE交AC于点F.
(1)求证:四边形ADCE为矩形;
(2)当△ABC满足什么条件时,四边形ADCE是一个正方形?并给出证明.
(3)在(2)的条件下,若AB=AC=2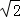 ,求正方形ADCE周长.
,求正方形ADCE周长.
查看答案和解析>>
科目:初中数学 来源: 题型:
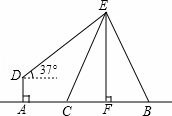
.如图,在电线杆上的E处引拉线EC和EB固定电线杆,在离电线杆6米的A处安置测角仪(点A,C,F在一直线上),在D处测得电线杆上E处的仰角为37°,已知测角仪的高AD为1.5米,AC为3米,求拉线EC的长.(精确到0.1米)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com