练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    如图，正三角形ABC（图1）和正五边形DEFGH（图2）的边长相同．点O为△ABC的中心，用5个相同的△BOC拼入正五边形DEFGH中，得到图3，则图3中的五角星的五个锐角均为（　　）

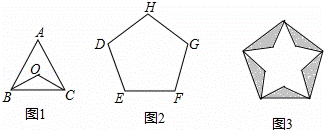
    　 A． 36° B． 42° C． 45° D． 48°


    D

    考点： 多边形内角与外角；等边三角形的性质． 

    分析： 根据图1先求出正三角形ABC内大钝角的度数是120°，则两锐角的和等于60°，正五边形的内角和是540°，求出每一个内角的度数，然后解答即可．

    解答： 解：如图，图1先求出正三角形ABC内大钝角的度数是180°﹣30°×2=120°，

    180°﹣120°=60°，

    60°÷2=30°，

    正五边形的每一个内角=（5﹣2）•180°÷5=108°，

    ∴图3中的五角星的五个锐角均为：108°﹣60°=48°．

    故选：D．

    点评： 本题主要考查了多边形的内角与外角的性质，仔细观察图形是解题的关键，难度中等．

    　


    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：


    （﹣5）×（﹣8）﹣（﹣28）÷4

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    下面这几个车标中，是中心对称图形而不是轴对称图形的共有（　　）

    第5题图
     

    A．1个    B．2个   C．3个   D．4个

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    某宾馆有40个房间供游客住宿，当每个房间的房价为每天160元时，房间会全部住满．当每个房间每天的房价每增加10元时，就会有一个房间空闲．宾馆需对游客居住的每个房间每天支出40元的各种费用．根据规定，要提高房价，但每个房间每天的房价不得高于280元．设每个房间的房价调整为每天x元（x为10的正整数倍）．

    （1）设一天订住的房间数为y，直接写出y与x的函数关系式及自变量x的取值范围；

    （2）设宾馆一天的利润为w元，求w与x的函数关系式；

    （3）一天订住多少个房间时，宾馆的利润最大？最大利润是多少元？

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    若关于x的一元二次方程kx2﹣4x+2=0有两个不相等的实数根，则k的取值范围是（　　）

    　 A． k＜2 B． k≠0 C． k＜2且k≠0 D． k＞2

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    如图，在平面直角坐标系中，A点为直线y=x上一点，过A点作AB⊥x轴于B点，若OB=4，E是OB边上的一点，且OE=3，点P为线段AO上的动点，则△BEP周长的最小值为（　　）

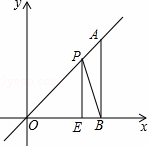
    　 A． 4+2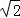 B． 4+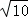 C． 6 D． 4

    查看答案和解析>>

    科目：初中数学 来源： 题型：


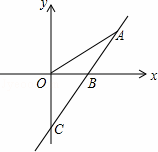
    如图，直线y=kx﹣4与x轴，y轴分别交于B、C两点．且∠OBC=．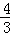

    （1）求点B的坐标及k的值；

    （2）若点A时第一象限内直线y=kx﹣4上一动点．则当△AOB的面积为6时，求点A的坐标；

    （3）在（2）成立的条件下．在坐标轴上找一点P，使得∠APC=90°，直接写出P点坐标．

    查看答案和解析>>

    科目：初中数学 来源： 题型：


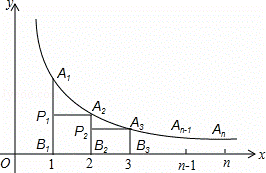
    如图，在反比例函数y=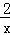（x＞0）的图象上有点A1，A2，A3，…，An﹣1，An，这些点的横坐标分别是1，2，3，…，n﹣1，n时，点A2的坐标是　　；过点A1作x轴的垂线，垂足为B1，再过点A2作A2P1⊥A1B1于点P1，以点P1、A1、A2为顶点的△P1A1A2的面积记为S1，按照以上方法继续作图，可以得到△P2A2A3，…，△Pn﹣1An﹣1An，其面积分别记为S2，…，Sn﹣1，则S1+S2+…+Sn=　　．

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    一个多项式减去等于，则这个多项式是

      A．    B．

      C．     D．

    查看答案和解析>>

    同步练习册答案