
【题目】已知:如图,在△ABC中,AB=BC=10,以AB为直径作⊙O分别交AC,BC于点D,E,连接DE和DB,过点E作EF⊥AB,垂足为F,交BD于点P.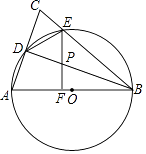
(1)求证:AD=DE;
(2)若CE=2,求线段CD的长;
(3)在(2)的条件下,求△DPE的面积.
【答案】
(1)证明:∵AB是⊙O的直径,
∴∠ADB=90°,
∵AB=BC,
∴D是AC的中点,∠ABD=∠CBD,
∴AD=DE;
(2)解:∵四边形ABED内接于⊙O,
∴∠CED=∠CAB,
∵∠C=∠C,
∴△CED∽△CAB,
∴ ![]() =
= ![]() ,
,
∵AB=BC=10,CE=2,D是AC的中点,
∴CD= ![]() ;
;
(3)解:延长EF交⊙O于M,
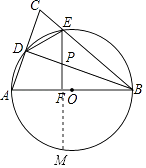
在Rt△ABD中,AD= ![]() ,AB=10,
,AB=10,
∴BD=3 ![]() ,
,
∵EM⊥AB,AB是⊙O的直径,
∴ ![]() =
= ![]() ,
,
∴∠BEP=∠EDB,
∴△BPE∽△BED,
∴ ![]() =
= ![]() ,
,
∴BP= ![]() ,
,
∴DP=BD﹣BP= ![]() ,
,
∴S△DPE:S△BPE=DP:BP=13:32,
∵S△BCD= ![]() ×
× ![]() ×3
×3 ![]() =15,S△BDE:S△BCD=BE:BC=4:5,
=15,S△BDE:S△BCD=BE:BC=4:5,
∴S△BDE=12,
∴S△DPE= ![]() .
.
【解析】(1)AD与DE都是弦,因此可证这两条弦所对的劣弧相等,进而可证弧所对的弦相等,由已知很容易根据等腰三角形性质和直径的性质得证;(2)求线段可采用相似法△CED∽△CAB,根据对应边成比例求出CD;(3)由已知底边、高都不易求,可转化为面积比法,即找一个面积易求的三角形,再求二者的比,通常找△DPE的等高三角形,底边在同一条直线上,它们的面积比等于底边长的比.


科目:初中数学 来源: 题型:
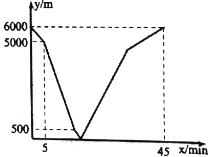
【题目】2019年3月31日,重庆举行了国际马拉松比赛,众多志愿者参与了服务工作,志愿者小茜和小悠分别从“南滨公园”和“朝天门桥”出发,沿同一条笔直的公路相向而行.小茜先出发5分钟后,小悠立刻骑自行车赶往“南滨公园”.小茜开始骑滑板车,中途改为跑步,且跑步的速度为滑板车速度的一半,到达“朝天门桥”时恰好用了45分钟.若两人之间的距离![]() 与小茜离开出发地的时间
与小茜离开出发地的时间![]() 之间的关系如图所示.则当小悠到达“南滨公园”时,小茜离“朝天门桥”的距离为__________米.
之间的关系如图所示.则当小悠到达“南滨公园”时,小茜离“朝天门桥”的距离为__________米.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在“植树节”期间,小王、小李两人想通过摸球的方式来决定谁去参加学校植树活动,规则如下:在两个盒子内分别装入标有数字1,2,3,4的四个和标有数字1,2,3的三个完全相同的小球,分别从两个盒子中各摸出一个球,如果所摸出的球上的数字之和小于6,那么小王去,否则就是小李去.
(1)用树状图或列表法求出小王去的概率;
(2)小李说:“这种规则不公平”,你认同他的说法吗?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
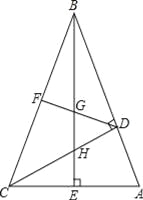
【题目】如图,在△ABC中,∠ABC=45°,CD⊥AB,BE⊥AC,垂足分别为D,E,F为BC中点,BE与DF,DC分别交于点G,H,∠ABE=∠CBE.
(1)线段BH与AC相等吗?若相等给予证明,若不相等请说明理由;
(2)求证:BG2﹣GE2=EA2.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,CD∥AB,点O在AB上,OE平分∠BOD,OF⊥OE,∠D=110°.

(1)求∠DOE的度数;
(2)OF平分∠AOD吗?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:用2辆A型车和1辆B型车装满货物一次可运货10吨;用1辆A型车和2辆B型车装满货物一次可运货11吨.某物流公司现有31吨货物,计划同时租用A型车![]() 辆,B型车
辆,B型车![]() 辆,一次运完,且恰好每辆车都装满货物. 根据以上信息,解答下列问题:
辆,一次运完,且恰好每辆车都装满货物. 根据以上信息,解答下列问题:
(1)1辆A型车和1辆B型车都装满货物一次可分别运货多少吨?
(2)请你帮该物流公司设计租车方案.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知点A,B,C,D,E,F是边长为1的正六边形的顶点,连接任意两点均可得到一条线段.在连接两点所得的所有线段中任取一条线段,取到长度为 ![]() 的线段的概率为( )
的线段的概率为( )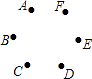
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com