【题目】如图，在平行四边形ABCD中，∠B＝30°，AB＝AC，O是两条对角线的交点，过点O作AC的垂线分别交边AD，BC于点E，F；点M是边AB的一个三等分点。则△AOE与△BMF的面积比为_________．
【答案】
【解析】连接MF，作AG⊥BC交BC于点G，作MH⊥BC交BC于点H，
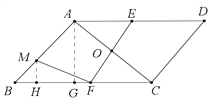
∵AB＝AC，∴∠B=∠ACB=30°，
设AB=AC=6x，则BM=2x，
∴MH=BM·sin30°=x，AG=AB·sin30°=3x，BG=AB·cos30°=3
x，
∵AB=AC，AG⊥BC，∴BG=CG=3x，BC=6x，
∵平行四边形ABCD，∴AD∥BC，OA=OC=3x，
∴∠EAO=∠ACB=30°，∴OE=OA·tan30°=x，AE=
=2x，
∴S△AOE=
OA·OE=
x2，
∵在△AOE和△COF中，
，
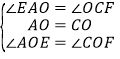∴△AOE≌△COF，
∴AE=CF=2x，
∴BF=6x－2x=4x，
∴S△BMF=BF·MH=2x2，
∴S△AOE∶S△BMF=(x2)∶(2x2)=3∶4.
故答案为3∶4.
科目：初中数学 来源： 题型：
【题目】已知任意三角形的三边长，如何求三角形面积？
古希腊的几何学家海伦解决了这个问题，在他的著作《度量论》一书中给出了计算公式﹣﹣海伦公式S= 
（其中a，b，c是三角形的三边长，p= 
，S为三角形的面积），并给出了证明
例如：在△ABC中，a=3，b=4，c=5，那么它的面积可以这样计算：
∵a=3，b=4，c=5
∴p= =6
∴S= = 
=6
事实上，对于已知三角形的三边长求三角形面积的问题，还可用我国南宋时期数学家秦九韶提出的秦九韶公式等方法解决．
如图，在△ABC中，BC=5，AC=6，AB=9
（1）用海伦公式求△ABC的面积；
（2）求△ABC的内切圆半径r．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，在Rt△ABC中，∠BAC＝90°，D是BC的中点，E是AD的中点，过点A作AF∥BC交BE的延长线于点F.
(1)求证：△AEF≌△DEB；
(2)求证：四边形ADCF是菱形；
(3)若AC＝4，AB＝5，求菱形ADCF的面积．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，在△ABC中，点D、E分别在边AB、AC上，DE∥BC，F为BC边上一点，连接AF交DE于点G，下列说法不正确的是（ ） 
A.
B.
C.
D.
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】菱形ABCD中，∠B=60°，延长BC至E，使得CE=BC，点F在DE上，DF=6，AG平分∠BAF，与线段BC相交于点G，若CG=2，则线段AB的长度为 ．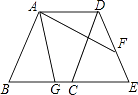 
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，均匀的正四面体的各面依次标有1，2，3，4四个数字．小明做了60次投掷试验，结果统计如下
：
朝下数字 | 1 | 2 | 3 | 4 |
出现的次数 | 16 | 20 | 14 | 10 |
（1）计算上述试验中“4朝下”的频率是多少？
（2）“根据试验结果，投掷一次正四面体，出现2朝下的概率是 
．”的说法正确吗？为什么？
（3）随机投掷正四面体两次，请用列表或画树状图法，求两次朝下的数字之和大于4的概率．
查看答案和解析>>
科目：初中数学 来源： 题型：
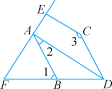
【题目】如图，已知∠1=∠BDC，∠2+∠3=180°．
（1）请你判断DA与CE的位置关系，并说明理由；
（2）若DA平分∠BDC，CE⊥AE于E，∠1=70°，试求∠FAB的度数．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】某中学积极开展“阳光体育”活动，共开设了跳绳、乒乓球、篮球、跑步四种运动项目．为了解学生最喜爱哪一种项目，随机抽取了部分学生进行调查，并绘制了如下的条形统计图和扇形统计图（部分信息未给出）
（1）求本次被调查的学生人数；
（2）补全条形统计图；
（3）根据统计的数据估计该中学3200名学生中最喜爱篮球的人数约有_____人．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，在△ABC和△A′B′C′中，AB=A′B′，∠B=∠B′，补充条件后仍不一定能保证△ABC≌△A′B′C′，则补充的这个条件是（ ）
A. BC=B′C′ B. ∠A=∠A′ C. AC=A′C′ D. ∠C=∠C′
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com