解:(1)全等的三角形有:△CBD≌△CA
1F或△AEF≌△B
1ED或△ACD≌△B
1CF等;
以证△CBD≌△CA
1F为例:
证明:∵∠ACB
1+∠A
1CF=∠ACB
1+∠BCD=90°
∴∠A
1CF=∠BCD
∵A
1C=BC
∴∠A
1=∠CBD=45°
∴△CBD≌△CA
1F;
(2)在△CBB
1中
∵CB=CB
1∴∠CBB
1=∠CB
1B=

(180°-α)
又△ABC是等腰直角三角形
∴∠ABC=45°
①若B
1B=B
1D,则∠B
1DB=∠B
1BD
∵∠B
1DB=45°+α
∠B
1BD=∠CBB
1-45°=

(180°-α)-45°=45°-

∴45°+α=45°-

,
∴α=0°(舍去);
②∵∠BB
1C=∠B
1BC>∠B
1BD,∴BD>B
1D,即BD≠B
1D;
③若BB
1=BD,则∠BDB
1=∠BB
1D,即45°+α=

(180°-α),α=30°
由①②③可知,当△BB
1D为等腰三角形时,α=30°;
(3)作DG⊥BC于G,设CG=x.
在Rt△CDG中,∠DCG=α=60°,
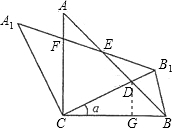
∴DG=xtan60°=

x
Rt△DGB中,∠DBG=45°,
∴BG=GD=

x,
∵AC=BC=1,
∴x+

x=1
∴x=
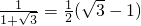
,
∴DB=

BG=

x=

×

=

.
分析:(1)依据全等三角形的判定,可找出全等的三角形有:△CBD≌△CA
1F或△AEF≌△B
1ED或△ACD≌△B
1CF等.由旋转的意义可证∠A
1CF=∠BCD,A
1C=BC,∠A
1=∠CBD=45°,所以△CBD≌△CA
1F.
(2)当△BBD是等腰三角形时,要分别讨论B
1B=B
1D、BB
1=BD、B
1D=DB三种情况,第一,三种情况不成立,只有第二种情况成立,求得α=30°.
(3)作DG⊥BC于G,在直角三角形CDG和直角三角形DGB中,由三角函数即可求得BD的长.
点评:本题考查了全等三角形的判定,综合应用直角三角形性质解直角三角形,进行逻辑推理能力和运算能力.

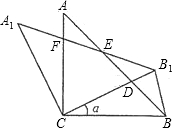 明(△ABC与△A1B1C1全等除外);
明(△ABC与△A1B1C1全等除外); (180°-α)
(180°-α) (180°-α)-45°=45°-
(180°-α)-45°=45°-
 ,
, (180°-α),α=30°
(180°-α),α=30°
 x
x x,
x, x=1
x=1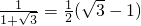 ,
, BG=
BG= x=
x= ×
× =
= .
.

 已知,如图,△ABC中,点D在BC上,且∠1=∠C,∠2=2∠3,∠BAC=70°.
已知,如图,△ABC中,点D在BC上,且∠1=∠C,∠2=2∠3,∠BAC=70°.